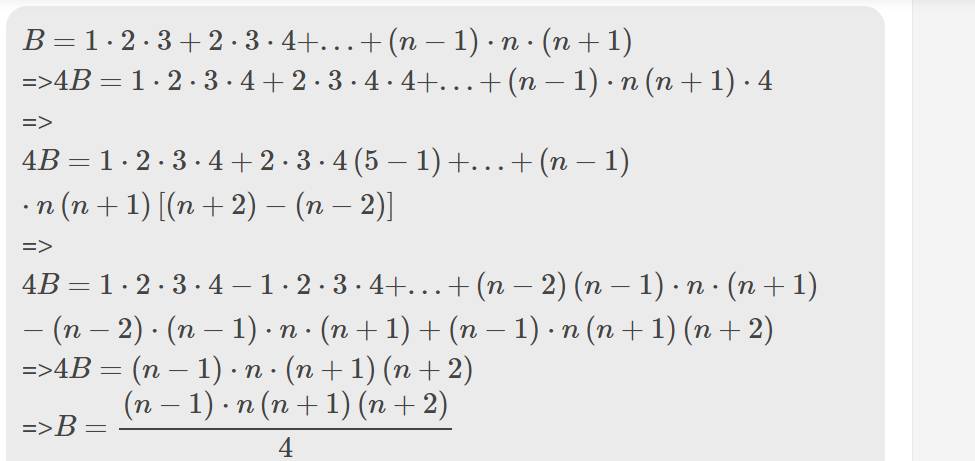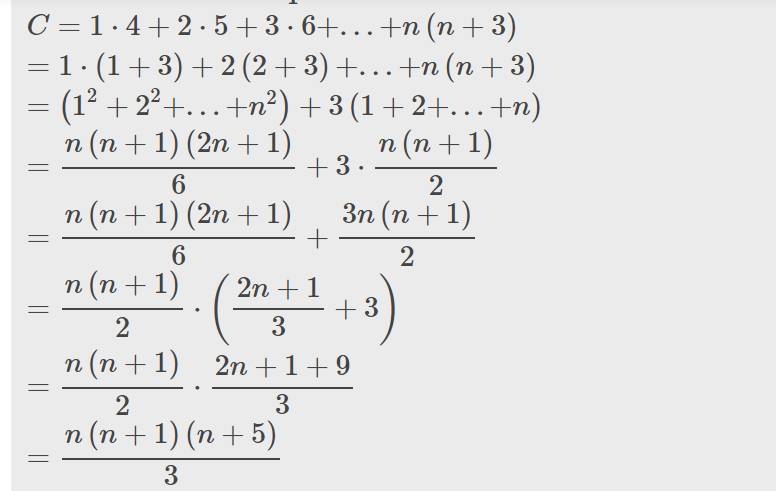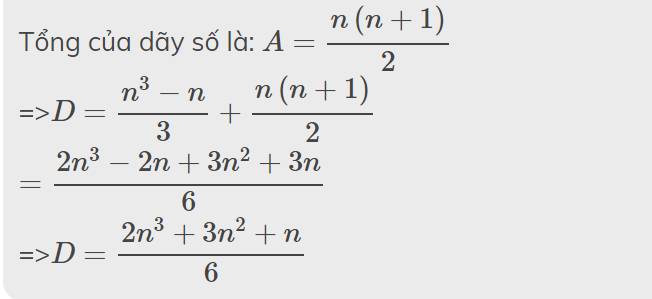K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
1
6 tháng 1 2017
A = 1.2.4 + 2.3.5 + ... + n(n+1)(n+3)
A = 1.2.(3+1) + 2.3.(4+1) + ... + n(n+1)[(n+2)+1]
A = [1.2.3 + 2.3.4 + ... + n(n+1)(n+2)] + [1.2 + 2.3 + ... + n(n+1)]
Đặt B = 1.2.3 + 2.3.4 + ... + n(n+1)(n+2)
4B = 1.2.3.(4-0) + 2.3.4.(5-1) + ... + n(n+1)(n+2)[(n+3)-(n-1)]
4B = 1.2.3.4 - 0.1.2.3 + 2.3.4.5 - 1.2.3.4 + ... + n(n+1)(n+2)(n+3) - (n-1)n(n+1)(n+2)
4B = n(n+1)(n+2)(n+3)
B = \(\frac{n\left(n+1\right)\left(n+2\right)\left(n+3\right)}{4}\)
Đặt C = 1.2 + 2.3 + ... + n(n+1)
3C = 1.2.(3-0) + 2.3.(4-1) + ... + n(n+1)[(n+2)-(n-1)]
3C = 1.2.3 - 0.1.2 + 2.3.4 - 1.2.3 + ... + n(n+1)(n+2) - (n-1)n(n+1)
3C = n(n+1)(n+2)
C = \(\frac{n\left(n+1\right)\left(n+2\right)}{3}\)
A = B + C = \(n\left(n+1\right)\left(n+2\right)\left(\frac{n+3}{4}+\frac{1}{3}\right)\)
\(=n\left(n+1\right)\left(n+2\right)\frac{3n+13}{12}\)
8 tháng 1 2017
tại sao bạn lại rút gọn được A = n(n+1)(n+2)(n+3/4+1/3) vậy
TN
0
13 tháng 11 2023
\(B=1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot4+...+\left(n-1\right)\cdot n\left(n+1\right)\cdot4\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\left(5-1\right)+...+\left(n-1\right)\cdot n\left(n+1\right)\left[\left(n+2\right)-\left(n-2\right)\right]\)
=>\(4B=1\cdot2\cdot3\cdot4-1\cdot2\cdot3\cdot4+...+\left(n-2\right)\left(n-1\right)\cdot n\cdot\left(n+1\right)-\left(n-2\right)\cdot\left(n-1\right)\cdot n\cdot\left(n+1\right)+\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)\)
=>\(4B=\left(n-1\right)\cdot n\cdot\left(n+1\right)\left(n+2\right)\)
=>\(B=\dfrac{\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)}{4}\)
\(C=1\cdot4+2\cdot5+3\cdot6+...+n\left(n+3\right)\)
\(=1\cdot\left(1+3\right)+2\left(2+3\right)+...+n\left(n+3\right)\)
\(=\left(1^2+2^2+...+n^2\right)+3\left(1+2+...+n\right)\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+3\cdot\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+\dfrac{3n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\left(\dfrac{2n+1}{3}+3\right)\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\dfrac{2n+1+9}{3}\)
\(=\dfrac{n\left(n+1\right)\left(n+5\right)}{3}\)
\(D=1^2+2^2+...+n^2\)
\(=1+\left(1+1\right)\cdot2+\left(1+2\right)\cdot3+...+\left(1+n-1\right)\cdot n\)
\(=1+2+3+...+n+\left(1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\right)\)
Đặt \(A=1+2+3+...+n;E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
\(E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot3+...+\left(n-1\right)\cdot n\cdot3\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+\left(n-1\right)\cdot n\left[\left(n+1\right)-\left(n-2\right)\right]\)
=>\(3E=1\cdot2\cdot3-1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\left(n-2\right)-\left(n-1\right)\cdot n\left(n-2\right)+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(3E=\left(n-1\right)\cdot n\left(n+1\right)=n^3-n\)
=>\(E=\dfrac{n^3-n}{3}\)
\(A=1+2+3+...+n\)
Số số hạng là n-1+1=n(số)
Tổng của dãy số là: \(A=\dfrac{n\left(n+1\right)}{2}\)
=>\(D=\dfrac{n^3-n}{3}+\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{2n^3-2n+3n^2+3n}{6}\)
=>\(D=\dfrac{2n^3+3n^2+n}{6}\)