K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 3 2016
Đặt A = 1/10 + 1/15 + 1/21 + ... + 1/66
=> 1/2.A = 1/20 + 1/30 + 1/42 + ... + 1/132
=> 1/2.A = 1/4.5 + 1/5.6 + 1/6.7 + ... + 1/11.12
=> 1/2.A = 1/4 - 1/5 + 1/5 - 1/6 + 1/6 - 1/7 + ... + 1/11 - 1/12
=> 1/2.A = 1/4 - 1/12
=> 1/2.A = 1/6
=> A = 1/6 : 1/2
=> A = 1/3
Vậy 1/10 + 1/15 + ... + 1/66 = 1/3
24 tháng 3 2016
Đặt A = 1/10 + 1/15 + 1/21 + ... + 1/66
=> 1/2.A = 1/20 + 1/30 + 1/42 + ... + 1/132
=> 1/2.A = 1/4.5 + 1/5.6 + 1/6.7 + ... + 1/11.12
=> 1/2.A = 1/4 - 1/5 + 1/5 - 1/6 + 1/6 - 1/7 + ... + 1/11 - 1/12
=> 1/2.A = 1/4 - 1/12
=> 1/2.A = 1/6
=> A = 1/6 : 1/2
=> A = 1/3
Vậy 1/10 + 1/15 + ... + 1/66 = 1/3
NT
3
Q
23 tháng 2 2016
xét: Sn = 1 + 2 + 3 + 4 + ... + n (1)
=> Sn = n + (n-1) + .. + 2 + 1 (2)
thấy 1+n = 2 + (n-1) = 3+(n-2) = n-1 + 2 = n+1
lấy (1) + (2) và với chú ý trên ta có:
2.Sn = (n+1) + (n+1) +..+ (n+1) = n(n+1) (vì n số hạng giống nhau)
=> Sn = n(n+1)/2 => Sn /n = (n+1)/2
=> P = 1 + S2/2 + S3/3 + S4/4 +...+ Sn /n
P = 1 + 3/2 + 4/2 + 5/2 +.. + (n+1)/2
P = 2(2 + 3 + 4 + ... + n + n+1) = 2(1+2 +..+ n+1) - 2 = 2.S(n+1) - 2
P = 2.(n+1)(n+2)/2 - 2 = (n+1)(n+2) - 2 = n²+3n
Bài toán chỉ tính đến S16/16 (tức n = 16)
P = 16² + 3.16 = ...
14 tháng 3 2016
xét: Sn = 1 + 2 + 3 + 4 + ... + n (1)
=> Sn = n + (n-1) + .. + 2 + 1 (2)
thấy 1+n = 2 + (n-1) = 3+(n-2) = n-1 + 2 = n+1
lấy (1) + (2) và với chú ý trên ta có:
2.Sn = (n+1) + (n+1) +..+ (n+1) = n(n+1) (vì n số hạng giống nhau)
=> Sn = n(n+1)/2 => Sn /n = (n+1)/2
=> P = 1 + S2/2 + S3/3 + S4/4 +...+ Sn /n
P = 1 + 3/2 + 4/2 + 5/2 +.. + (n+1)/2
P = 2(2 + 3 + 4 + ... + n + n+1) = 2(1+2 +..+ n+1) - 2 = 2.S(n+1) - 2
P = 2.(n+1)(n+2)/2 - 2 = (n+1)(n+2) - 2 = n²+3n
bài toán chỉ tính đến S16/16 (tức n = 16)
P = 16² + 3.16 = ...
ND
7
26 tháng 3 2016
B= 3/2.4/3. ....2001/2000
B = 3.4....2001/2.3....2000
B =2001/2
CM
1 tháng 2 2017
Phương pháp:
+) Kiểm tra tính liên tục của hàm số tại x = 1
+) Nếu hàm số liên tục tại x = 1, sử dụng công thức tính đạo hàm bằng định nghĩa:
HP
5 tháng 4 2016
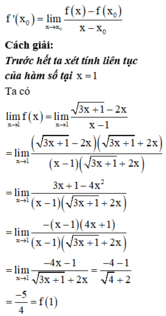
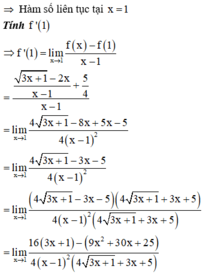
Đặt \(A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+......+\frac{1}{3^{50}}\)
=>\(3A=1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{49}}\)
=>\(3A-A=\left(1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{49}}\right)-\left(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+....+\frac{1}{3^{50}}\right)\)
=>2A=\(1-\frac{1}{3^{50}}\)
=>A=\(\frac{1-\frac{1}{3^{50}}}{2}\)
\(=>A=\frac{1}{2}-\frac{1}{\frac{3^{50}}{2}}=\frac{1}{2}-1.\frac{2}{3^{50}}=\frac{1}{2}-\frac{2}{3^{50}}=\frac{3^{50}-4}{2.3^{50}}\)
Vậy..................
5 tháng 4 2016
Xin lỗix nha mình chỉ biết kết qur thôi chứ ko biết cách giải chi tiết.
Nếu kết quả thì là \(-\frac{7}{2}\)
CM
13 tháng 6 2017
Ta có
z = 1 + i 21 - 1 1 + i - 1 = 1 + i 21 - 1 i = 1 + i 2 10 1 + i - 1 i = - 2 10 + 2 10 + 1 i .
Vậy tổng phần thực và phần ảo của số phức z bằng 1
Đáp án A
10 tháng 3 2016
Đáp án
Bài giải qua 3 bước như sau:
Bước 1: Xét mẫu số của số hạng tổng quát trong tổng trên:
S = 1 + 2 + ... + (n - 1) + n ( * )
Khi viết S theo thứ tự ngược lại la có:
S = n + (n - 1) + ... + 2 + 1 ( ** )
Cộng vế với vế của ( * ) và ( ** ) ta có:
S + S = [1 + n] + [2 + (n - 1)] + ... + [(n - 1) + 2] + [n + 1]
2 . S = [n + 1] + [n + 1] + . . . + [n + 1] + [n + 1] (Tổng có n số hạng [n + 1] )
2 . S = n.(n + 1)
=> S = n.(n + 1)/2
=> Số hạng tổng quát của tổng đã cho là:
Bước 2: Ta có nhận xét:
=> ( *** )
Bước 3: Thay n = 1, 2, ... vào ( *** ) ta được các đẳng thức tương ứng:
. . .
Cộng các vế với nhau ta được:
Vậy tổng đã cho có kết quả bằng 2.
HP
10 tháng 3 2016
Đặng Thị Thùy Linh copy đáp án trên OLM
bn có thể vào mục "toán vui mỗi tuần" của OLM
1/50x51+1/51x52+.....+1/99x100
ta rút gọn còn: 1/50+1/100
= 2/100+1/100
= 3/100
3/100