Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số y = f(x) = x4 - 3x2 + 1 có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa f(-x) = (-x)4 - 3(-x)2 + 1 = x4 - 3x2 + 1 = f(x), nên y = f(x) là hàm số chẵn.
b) Hàm số y = g(x) = -2x3 + x có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa g(-x) = -2(-x)3 + (-x) = 2x3 - x = -g(x), nên y = g(x) là hàm số lẻ.
c) Hàm số y = h(x) =|x + 2|- |x - 2 | có tập xác định D là R, do đó ∀ x ∈ D thì –x ∈ D, hơn nữa h(-x) = | -x + 2| -|-x – 2|= |x - 2| - |x + 2|= -(|x + 2| - |x - 2 |) = -h{x)
Vì vậy y = h(x) là hàm số lẻ.
d) Chứng minh tương tự ta có y = |2x + 1| + |2x — 1| là hàm số chẵn.

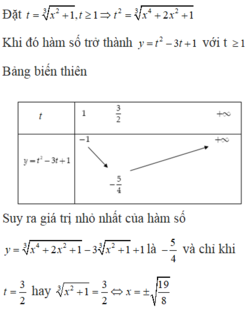
Đặt ![]()
Khi đó hàm số trở thành y= t2- 3t+1 với t≥ 1.
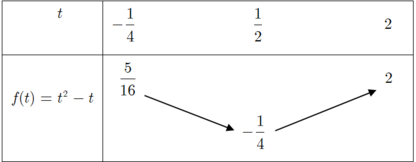
Bảng biến thiên
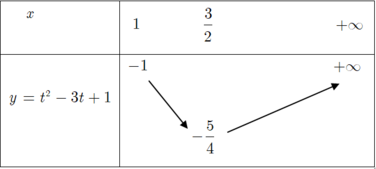
Suy ra giá trị nhỏ nhất của hàm số:
![]()
khi và chỉ khi t= 3/2 hay 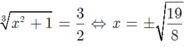
Chọn C.

\(\sqrt{4x-5}=1-2x\)
Điều kiện: \(4x-5\) ≥ \(0\) ⇔ \(x\) ≥ \(\dfrac{5}{4}\)
PT ⇔ \(4x-5=\left(1-2x\right)^2\)
⇔ \(4x-5=1-4x+4x^2\)
⇔ \(4x^2-8x+6=0\)
⇔ Phương trình vô nghiệm
\(\left|5x^2-11\right|=x-5\)
TH1: \(5x^2-11=x-5\)
⇔ \(5x^2-x-6=0\)
⇔ \(\left[{}\begin{matrix}x=\dfrac{6}{5}\\x=-1\end{matrix}\right.\) (Loại)
TH2: \(5x^2-11=-x+5\)
⇔ \(5x^2+x-16=0\)
⇔ \(\left[{}\begin{matrix}x=\dfrac{-1+\sqrt{321}}{10}\\x=\dfrac{-1-\sqrt{321}}{10}\end{matrix}\right.\)(Thỏa mãn)
Vậy \(x=\dfrac{-1+\sqrt{321}}{10}\) và \(x=\dfrac{-1-\sqrt{321}}{10}\) là 2 nghiệm của phương trình.
\(x^4-3x^2-28=0\)
Đặt: \(t=x^2\) (\(t\) ≥ \(0\))
Ta được: \(t^2-3t-28=0\)
⇔ \(\left[{}\begin{matrix}t=7\\t=-4\end{matrix}\right.\)
Với \(t=7\) ⇒ \(x^2=7\)
⇔ \(\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\)
Vậy \(x=\sqrt{7}\) và \(x=-\sqrt{7}\) là nghiệm của phương trình.

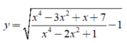 xác định khi và chỉ khi
xác định khi và chỉ khi
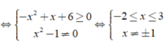
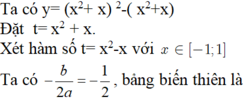
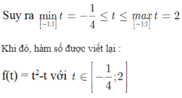
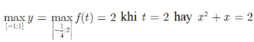
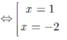
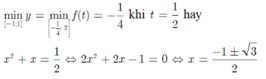
a: \(x\in\left[-2;3\right]\)
nên \(\left\{{}\begin{matrix}x^4\in\left[0;81\right]\\x^2\in\left[0;9\right]\end{matrix}\right.\Leftrightarrow x^4+3x^2\in\left[0;108\right]\)
=>\(y\in\left[2;110\right]\)
y=2 khi x=0
y=110 khi \(x^4+3x^2=108\)
=>x^4+12x^2-9x^2-108=0
=>x=3
c: \(y=x\left(x+3\right)\left(x+1\right)\left(x+2\right)\)
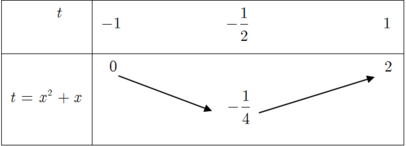
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1-1\)
\(=\left(x^2+3x+1\right)^2-1>=-1\)
Dấu'=' xảy ra khi x^2+3x+1=0
hay \(x\in\left\{\dfrac{-3+\sqrt{5}}{2};\dfrac{-3-\sqrt{5}}{2}\right\}\)