NP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 12 2017
a) x:y:z:t=2:3:4:5
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}\)
Áp dụng tính ... , ta có :
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}=\frac{x+y+z+t}{2+3+4+5}=\frac{-42}{14}=-3\)
\(\Rightarrow x=-6;y=-9;z=-12;t=-15\)
b) c ) tương tự
22 tháng 12 2018
mk chỉ đăng thek thôi mà
nếu ko muốn làm thì thôi đừng ở đó mà ns như làm ra vẻ
12 tháng 9 2021
x; y ; z lần lượt tỉ lệ với 5 ; 3 ; 2\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}=\dfrac{x+y-z}{5+3-2}=\dfrac{36}{6}=6\)
\(\dfrac{x}{5}=6\Rightarrow x=30\\ \dfrac{y}{3}=6\Rightarrow y=18\\ \dfrac{z}{2}=6\Rightarrow z=12\)
Vậy ...
17 tháng 11 2016
y tỉ lệ thuận với x theo hệ số tỉ lệ là 3 nên ta có
y=3x (1)
x tỉ lệ thuận vói z theo hệ số tỉ lệ là -4 nên ta có
x =-4z (2)
Thay điều (2) vào điều (1)
y=3(-4z)
y=(-4.3).z
y=-12z
Vậy y và z có tỉ lệ thuận với nhau theo hệ số tỉ lệ là -12
Công thức khái quát
y=(hk)x
Mình không biết công thức khái quát mình viết có đúng hay sai không nữa.
DD
Đoàn Đức Hà
Giáo viên
25 tháng 10 2021
\(x\)và \(y\)tỉ lệ thuận với \(2\)và \(5\)nên \(\frac{x}{2}=\frac{y}{5}\).
\(y\)và \(z\)tỉ lệ nghịch với \(3\)và \(4\)nên \(\frac{y}{4}=\frac{z}{3}\).
\(\hept{\begin{cases}\frac{x}{2}=\frac{y}{5}\\\frac{y}{4}=\frac{z}{3}\end{cases}}\Leftrightarrow\frac{x}{8}=\frac{y}{20}=\frac{z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{8}=\frac{y}{20}=\frac{z}{15}=\frac{x-y+z}{8-20+15}=\frac{36}{3}=12\)
\(\Leftrightarrow\hept{\begin{cases}x=12.8=96\\y=12.20=240\\z=12.15=180\end{cases}}\)
22 tháng 2 2020
a, Ta có : \(\frac{x}{3}=\frac{y}{5}\)
- Áp dụng tính chất của dãy tỉ số bằng nhau .
\(\frac{x}{3}=\frac{y}{5}=\frac{x-y}{3-5}=\frac{-4}{-2}=2\)
=> \(\left\{{}\begin{matrix}\frac{x}{3}=2\\\frac{y}{5}=2\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=6\\y=10\end{matrix}\right.\)
Vậy giá trị của x = 6, y = 10 .
b, Ta có : \(\frac{x}{5}=\frac{y}{4}\)
- Áp dụng tính chất của dãy tỉ số bằng nhau .
\(\frac{x}{5}=\frac{y}{4}=\frac{x-y}{5-4}=\frac{3}{1}=3\)
=> \(\left\{{}\begin{matrix}\frac{x}{5}=3\\\frac{y}{4}=3\\\frac{z}{3}=3\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=15\\y=12\\z=9\end{matrix}\right.\)
Vậy giá trị của x = 15, y = 12 ,z = 9
a, Ta có : \(x:y:z:t=2:3:4:5\)
=> \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}\)
- Áp dụng tính chất của dãy tỉ số bằng nhau .
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}=\frac{x+y+z+t}{2+3+4+5}=\frac{-42}{14}=-3\)
=> \(\left\{{}\begin{matrix}\frac{x}{2}=-3\\\frac{y}{3}=-3\\\frac{z}{4}=-3\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=-6\\y=-9\\z=-12\end{matrix}\right.\)
Vậy giá trị của x = -6, y = -9, z = -12 .
28 tháng 9 2016
Câu 1:
a)Áp dụng tc dãy tỉ:
\(\frac{x}{3}=\frac{y}{7}=\frac{x+y}{3+7}=\frac{20}{10}=2\)
\(\Rightarrow\begin{cases}\frac{x}{3}=2\Rightarrow x=6\\\frac{y}{7}=2\Rightarrow y=14\end{cases}\)
b)Áp dụng tc dãy tỉ:
\(\frac{x}{5}=\frac{y}{2}=\frac{x-y}{5-2}=\frac{6}{3}=2\)
\(\Rightarrow\begin{cases}\frac{x}{5}=2\Rightarrow x=10\\\frac{y}{2}=2\Rightarrow y=4\end{cases}\)
Câu 2:
a)\(\frac{x}{7}=\frac{18}{14}\Rightarrow14x=18\cdot7\)
\(\Rightarrow14x=126\)
\(\Rightarrow x=9\)
b và c đề có vấn đề
28 tháng 9 2016
Câu 1:
a) Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{7}=\frac{x+y}{3+7}=\frac{20}{10}=2\)
+) \(\frac{x}{3}=2\Rightarrow x=6\)
+) \(\frac{y}{7}=2\Rightarrow y=14\)
Vậy cặp số \(\left(x,y\right)\) là \(\left(6,14\right)\)
b) Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{5}=\frac{y}{2}=\frac{x-y}{5-2}=\frac{6}{3}=2\)
+) \(\frac{x}{5}=2\Rightarrow x=10\)
+) \(\frac{y}{2}=2\Rightarrow y=4\)
Vậy cặp số \(\left(x,y\right)\) là \(\left(10,4\right)\)
Câu 3:
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}=\frac{x-y+z}{2-4+6}=\frac{8}{4}=2\)
+) \(\frac{x}{2}=2\Rightarrow x=4\)
+) \(\frac{y}{4}=2\Rightarrow y=8\)
+) \(\frac{z}{6}=2\Rightarrow z=12\)
Vậy bộ số \(\left(x,y,z\right)\) là \(\left(4,8,12\right)\)
Câu 4:
Giải:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow a=bk,c=dk\)
Ta có:
\(\frac{a+b}{a-b}=\frac{bk+b}{bk-b}=\frac{b\left(k+1\right)}{b\left(k-1\right)}=\frac{k+1}{k-1}\) (1)
\(\frac{c+d}{c-d}=\frac{dk+d}{dk-d}=\frac{d\left(k+1\right)}{d\left(k-1\right)}=\frac{k+1}{k-1}\) (2)
Từ (1) và (2) suy ra \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
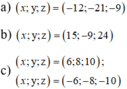
Ý bạn hỏi là?
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x-y}{5-4}=\frac{3}{1}=3\)
\(\frac{x}{5}=3\Rightarrow x=3.5=15\)
\(\frac{y}{4}=3\Rightarrow y=3.4=12\)
\(\frac{z}{3}=3\Rightarrow z=3.3=9\)
Vậy x=15 ; y=12 và z=9