K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VL
1
S
3 tháng 12 2019
1)
Có:\(\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{y}{12}\\\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{y}{12}=\frac{z}{15}\end{cases}\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}}\)
Áp dụng tc của DTSBN có:
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x-y+z}{8-12+15}=\frac{33}{11}=3\) (vì x-y+z=33)
\(\Rightarrow\hept{\begin{cases}x=3.8=24\\y=3.12=36\\y=3.15=45\end{cases}}\)(tm)
Vậy.....................
2)
Có: \(\text{ x:y:z=2:3:4 }\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\Rightarrow\frac{x}{2}=\frac{3y}{9}=\frac{2z}{8}\)
Áp dụng tc của DTSBN có:
\(\frac{x}{2}=\frac{3y}{9}=\frac{2z}{8}=\frac{x+3y-2z}{2+9-8}=\frac{3}{3}=1\)(vì x+3y-z=3)
\(\Rightarrow\hept{\begin{cases}x=2\\y=3\\z=4\end{cases}}\)(tm)
Vậy................
21 tháng 9 2018
1, \(x\div y\div z=3\div8\div5\)
\(\Rightarrow\frac{x}{3}=\frac{y}{8}=\frac{z}{5}\)
\(\Rightarrow\frac{3x}{9}=\frac{y}{8}=\frac{2z}{10}\)
\(\Rightarrow\frac{3x+y-2z}{9+8-10}=\frac{x}{3}=\frac{y}{8}=\frac{z}{10}=\frac{14}{7}=2\)
\(\Rightarrow\hept{\begin{cases}x=2\cdot3=6\\y=2\cdot8=16\\z=2\cdot5=10\end{cases}}\)
vậy_
các phần sau tương tự
HN
21 tháng 9 2018
1, \(x:y:z=3:8:5;3x+y-2z=14\)
\(\Rightarrow\frac{x}{3}=\frac{y}{8}=\frac{z}{5}\)
\(\Rightarrow\frac{3x}{9}=\frac{y}{8}=\frac{2z}{10}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3x}{9}=\frac{y}{8}=\frac{2z}{10}=\frac{3x+y-2z}{9+8-10}=\frac{14}{7}=2\)
\(\Rightarrow\hept{\begin{cases}\frac{3x}{9}=2\Rightarrow3x=18\Rightarrow x=6\\\frac{y}{8}=2\Rightarrow y=16\\\frac{2z}{10}=2\Rightarrow2z=20\Rightarrow z=10\end{cases}}\)
Vậy....
2, \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3};4x-3y-2z=36\)
\(\Rightarrow\frac{4x}{4}=\frac{3y}{6}=\frac{2z}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{4x}{4}=\frac{3y}{6}=\frac{2z}{6}=\frac{4x-3y-2z}{4-6-6}=\frac{36}{-8}=\frac{-36}{8}=\frac{-9}{4}\)
Làm tương tự để tìm x;y;z
3, \(x:y:z=3:5:\left(-2\right);5x-y+3z=124\)
\(\Rightarrow\frac{x}{3}=\frac{y}{5}=\frac{z}{\left(-2\right)}\)
\(\Rightarrow\frac{5x}{15}=\frac{y}{5}=\frac{3z}{-6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{5x}{15}=\frac{y}{5}=\frac{3z}{-6}=\frac{5x-y+3z}{15-5+\left(-6\right)}=\frac{124}{4}=31\)
\(\Rightarrow\hept{\begin{cases}\frac{5x}{15}=31\Rightarrow5x=465\Rightarrow x=93\\\frac{y}{5}=31\Rightarrow y=155\\\frac{3z}{-6}=31\Rightarrow3z=-186\Rightarrow z=-62\end{cases}}\)
Vậy .....
NT
2
TH
14 tháng 10 2016
Vì x:y:z=2:3:4
=>x/2=y/3=z/4=2z/8
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/2=y/3=z/4=x+y-2z/2+3-8=3/-3=-1
Do đó: x/2=-1=>x=-2
y/3=-1=>y=-3
z/4=-1=>z=-4
30 tháng 11 2019
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{2z}{8}\)
x+y-2z=3
áp dụng ta có:
\(\frac{x+y-2z}{2+3-8}=\frac{3}{-3}=-1\)
suy ra:
\(\frac{x}{2}=-1...x=-2\) tương tự với y và z.
29 tháng 10 2016
1.\(\frac{x}{y}=\frac{2}{3}\Rightarrow\frac{x}{2}=\frac{y}{3}\Rightarrow\hept{\begin{cases}\frac{x}{2}.\frac{y}{3}=\frac{54}{6}=9\\\frac{x}{2}.\frac{y}{3}=\left(\frac{x}{2}\right)^2=\left(\frac{y}{3}\right)^2\end{cases}\Rightarrow\left(\frac{x}{2}\right)^2}=\left(\frac{y}{3}\right)^2=9\Rightarrow\orbr{\begin{cases}\frac{x}{2}=\frac{y}{3}=3\\\frac{x}{2}=\frac{y}{3}=-3\end{cases}\Rightarrow\orbr{\begin{cases}x=6;y=9\\x=-6;y=-9\end{cases}}}\)
2.\(x:y:z=3:8:5\Rightarrow\frac{x}{3}=\frac{y}{8}=\frac{z}{5}=\frac{3x}{9}=\frac{2z}{10}=\frac{3x+y-2z}{9+8-10}=\frac{14}{7}=2\Rightarrow\hept{\begin{cases}x=2.3=6\\y=2.8=16\\z=2.5=10\end{cases}}\)
NT
0
NQ
0
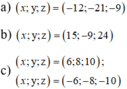
\(x:y:z=2:3:4\)
\(\Rightarrow\)\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y-2z}{2+3-8}=\frac{3}{-3}=-1\)
\(\Rightarrow\)\(x=-1.2=-2\)
\(\Rightarrow\)\(y=-1.3=-3\)
\(\Rightarrow\)\(z=-1.4=-4\)
x : y : z = 2 : 3 : 4
=> x/2 = y/3 = z/4
=> x/2 = y/3 = 2z/8
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có :
x/2 = y/3 = 2z/8 = x+y-2z/2+3-8 = 3/-3 = -1
=> x = -2 ; y = -3 ; z = -4