
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có 2x -1 và 3x-9 thuộc Z vì x và y thuộc Z
=> 12 chia hết cho 2x-1
mà 2x-1 lẻ => 2x-1=-1;-3;1;3
=> x=0;-1;1;2
=> y=.........



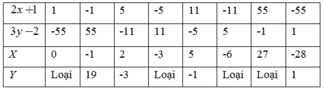
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
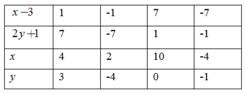
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.

Vì (x+1)(2y-1)=12 nên x+1 và 2y-1 thuộc Ư(12)
Ư(12)={-12;-6;-4;-3;-2;-1;1;2;3;4;6;12}
Ta có bảng:
| x+1 | -1 | -2 | -3 | -4 | -6 | -12 | 1 | 2 | 3 | 4 | 6 | 12 |
| x | -2 | -3 | -4 | -5 | -7 | -13 | 0 | 1 | 2 | 3 | 5 | 11 |
| 2y-1 | -12 | -6 | -4 | -3 | -2 | -1 | 12 | 6 | 4 | 3 | 2 | 1 |
| 2y | -11 | -5 | -3 | -2 | -1 | 0 | 13 | 7 | 5 | 4 | 3 | 2 |
| y | (loại) | loại | loại | -1 | loại | 0 | loại | loại | loại | 2 | loại | 1 |

Lời giải:
Với $x,y$ nguyên thì $3x+1, 2y-3$ là số nguyên.
Mà $(2x+1)(2y-3)=12$ nên $2y-3$ là ước của $12$.
Mà $2y-3$ lẻ nên $2y-3\in \left\{\pm 1; \pm 3\right\}$
Nếu $2y-3=1\Rightarrow 3x+1=12$
$\Rightarrow x=\frac{11}{3}$ (loại)
Nếu $2y-3=-1\Rightarrow 3x+1=-12\Rightarrow x=\frac{-13}{3}$ (loại)
Nếu $2y-3=3\Rightarrow 3x+1=4$
$\Rightarrow y=3; x=1$ (thỏa mãn)
Nếu $2y-3=-3\Rightarrow 3x+1=-4$
$\Rightarrow x=\frac{-5}{3}$ (loại)
Vậy..........