K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
2
27 tháng 7 2021
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
4 tháng 9 2020
\(\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}=0\)
Vì \(\hept{\begin{cases}\left(x+1\right)^{2020}\ge0\forall x\\\left(2-3y\right)^{2022}\ge0\forall y\end{cases}}\Rightarrow\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}\ge0\forall x,y\)
Dấu " = " xảy ra khi và chỉ khi \(\hept{\begin{cases}\left(x+1\right)^{2020}=0\\\left(2-3y\right)^{2022}=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\3y=2\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\y=\frac{2}{3}\end{cases}}\)
4 tháng 9 2020
( x + 1 )2020 + ( 2 - 3y )2022 = 0
Ta có \(\hept{\begin{cases}\left(x+1\right)^{2020}\ge0\forall x\\\left(2-3y\right)^{2022}\ge0\forall y\end{cases}}\Rightarrow\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}\ge0\forall x,y\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x+1=0\\2-3y=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\y=\frac{2}{3}\end{cases}}\)
Vậy x = -1 ; y = 2/3
LT
0
ND
Nguyễn Đức Trí
VIP
29 tháng 7 2023
\(\left(2x\right)^2-y^2=-8\)
\(\Rightarrow4x^2-y^2=-8\)
\(\Rightarrow\left(2x-y\right)\left(2x+y\right)=-8\)
\(\Rightarrow\left(2x-y\right);\left(2x+y\right)\in=\left\{-1;1;-2;2;-4;4;-8;8\right\}\)
\(\Rightarrow\left(x;y\right)\in=\left\{\left(\dfrac{7}{4};\dfrac{9}{2}\right);\left(-\dfrac{7}{4};-\dfrac{9}{2}\right);\left(\dfrac{1}{2};3\right);\left(-\dfrac{1}{2};-3\right);\left(-\dfrac{1}{2};3\right)\left(\dfrac{1}{2};-3\right);\left(-\dfrac{7}{4};\dfrac{9}{2}\right);\left(\dfrac{7}{4};-\dfrac{9}{2}\right)\right\}\)
20 tháng 3 2017
9-x^2=5(y+3)^2
vì 5(y+3)^2 >hoặc bằng 0
suy ra 9-x^2 lớn hơn hoặc bằng 0
suy ra x^2 bé hơn hoặc bằng 9
suy ra x =1 , x=2 hoặc x=3
thay x vào rồi tự tính y nha bạn !!!!!
S
29 tháng 3 2023
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{x}=\dfrac{x+y+z}{y+z+x}=\dfrac{x+y+z}{x+y+z}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\)
Do đó \(\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\)
Thay vào biểu thức \(P=\left(x-y\right)^{2022}+\left(y-z\right)^{2023}+\left(x-z-1\right)^{202}\),ta có:
\(P=0^{2022}+0^{2023}+\left(-1\right)^{202}\)
\(=0+0+1\)
\(=1\)
B
tìm x,y,z thuộc Q biết :
a)x(x-y+z)=-11
y(y-z-x)=25
z(z+x-y)=35
b)(c+2) mũ 2+(y-3) mũ 4 +(z-5) mũ 6 =0
0
5 tháng 7 2023
Nhóm 1: 5x^2y^3;x^2y^3;1/2x^2y^3;x^2y^3
Tổng là 6,5x^2y^3
Nhóm 2: 10x^3y^2;-3x^3y^2;-5x^3y^2
Tổng là 2x^3y^2
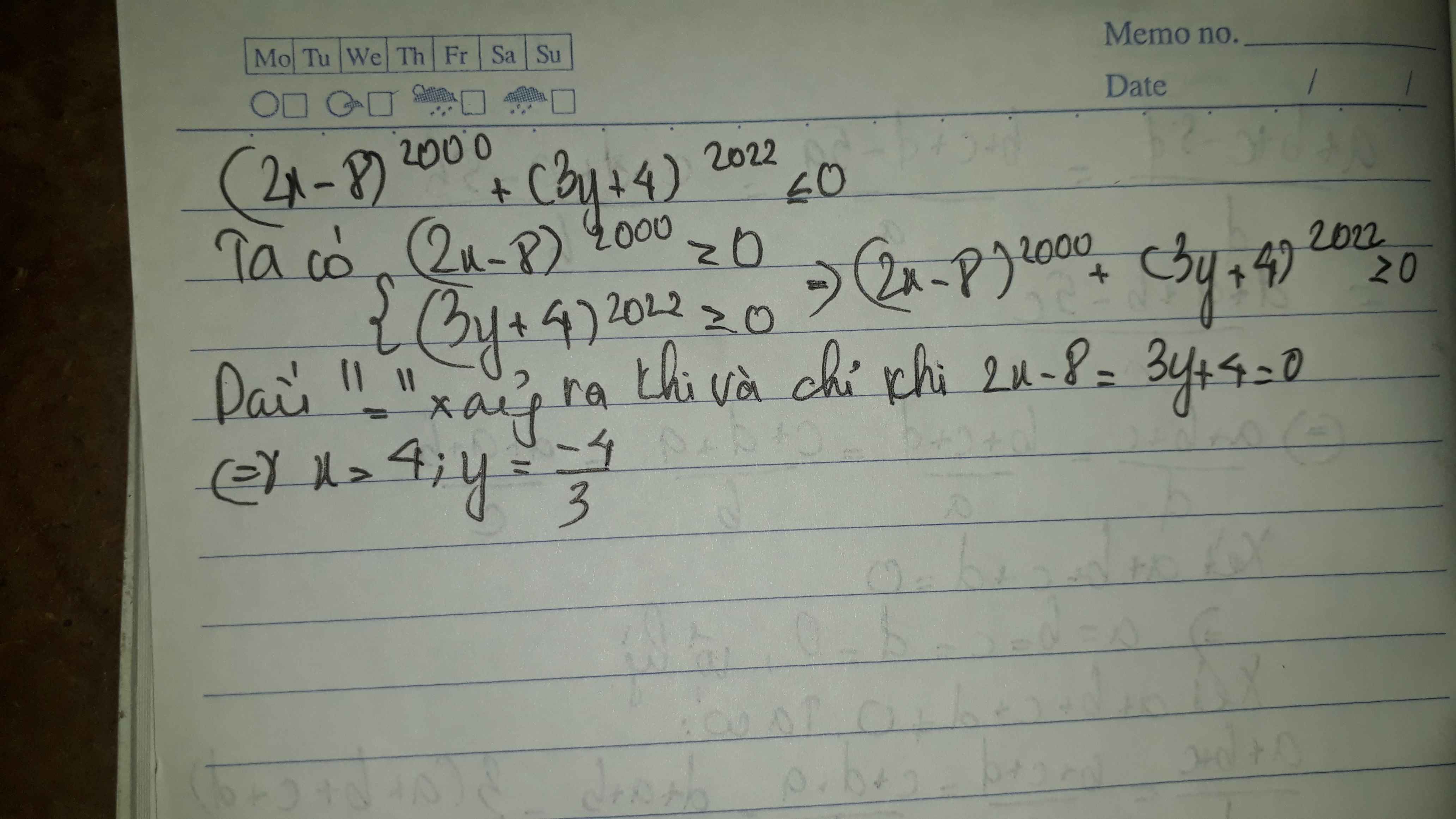
khó quá các bạn giúp mình nhé!
Tham khảo:
https://hoidap247.com/cau-hoi/5161344