FG
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 10 2023
a: \(x\left(1-2x\right)+2x^2=14\)
=>\(x-2x^2+2x^2=14\)
=>x=14
b: \(x\left(x-5\right)+3x-15=0\)
=>\(\left(x-5\right)\left(x+3\right)=0\)
=>\(\left[{}\begin{matrix}x-5=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)
7 tháng 1 2023
Bài 2:
x^3+6x^2+12x+m chia hết cho x+2
=>x^3+2x^2+4x^2+8x+4x+8+m-8 chia hết cho x+2
=>m-8=0
=>m=8
AH
Akai Haruma
Giáo viên
26 tháng 10 2023
Lời giải:
1.
$x^3+3x^2-16x-48=(x^3+3x^2)-(16x+48)=x^2(x+3)-16(x+3)$
$=(x+3)(x^2-16)=(x+3)(x-4)(x+4)$
2.
$4x(x-3y)+12y(3y-x)=4x(x-3y)-12y(x-3y)=(x-3y)(4x-12y)=4(x-3y)(x-3y)=4(x-3y)^2$
3.
$x^3+2x^2-2x-1=(x^3-x^2)+(3x^2-3x)+(x-1)=x^2(x-1)+3x(x-1)+(x-1)$
$=(x-1)(x^2+3x+1)$
2
10 tháng 1 2023
`a)2x^2+3(x-1)(x+1)=5x(x+1)`
`<=>2x^2+3x^2-3=5x^2+5x`
`<=>5x=-3`
`<=>x=-3/5`
__________________________________________
`b)(x-3)^3+3-x=0` nhỉ?
`<=>(x-3)^3-(x-3)=0`
`<=>(x-3)(x^2-1)=0`
`<=>[(x=3),(x^2=1<=>x=+-1):}`
__________________________________________
`c)5x(x-2000)-x+2000=0`
`<=>5x(x-2000)-(x-2000)=0`
`<=>(x-2000)(5x-1)=0`
`<=>[(x=2000),(x=1/5):}`
__________________________________________
`d)3(2x-3)+2(2-x)=-3`
`<=>6x-9+4-2x=-3`
`<=>4x=2`
`<=>x=1/2`
__________________________________________
`e)x+6x^2=0`
`<=>x(1+6x)=0`
`<=>[(x=0),(x=-1/6):}`
19 tháng 4 2023
2:
a: =>x-1=0 hoặc 3x+1=0
=>x=1 hoặc x=-1/3
b: =>x-5=0 hoặc 7-x=0
=>x=5 hoặc x=7
c: =>\(\left[{}\begin{matrix}x-1=0\\x+5=0\\3x-8=0\end{matrix}\right.\Leftrightarrow x\in\left\{1;-5;\dfrac{8}{3}\right\}\)
d: =>x=0 hoặc x^2-1=0
=>\(x\in\left\{0;1;-1\right\}\)
HP
15 tháng 9 2021
a. (2x + 1)2 - 4x2 + 2x2 - 2 = 0
<=> (2x + 1 - 2x)(2x + 1 + 2x) + 2(x2 - 1) = 0
<=> (4x + 1) + 2x2 - 2 = 0
<=> 4x + 1 + 2x2 - 2 = 0
<=> 2x2 + 4x - 2 + 1 = 0
<=> 2x2 + 4x - 1 = 0
<=> 2x2 + 4x = 1
<=> 2x(x + 2) = 1
Vì 1 chỉ có tích là 1 . 1 nên:
<=> \(\left[{}\begin{matrix}2x=1\\x+2=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
15 tháng 9 2021
\(a,\Leftrightarrow4x^2+4x+1-4x^2+2x^2-2=0\\ \Leftrightarrow2x^2+4x-1=0\\ \Leftrightarrow2\left(x^2+2x+1\right)-3=0\\ \Leftrightarrow2\left(x+1\right)^2-3=0\\ \Leftrightarrow\left(x+1\right)^2=\dfrac{3}{2}\\ \Leftrightarrow\left[{}\begin{matrix}x+1=\sqrt{\dfrac{3}{2}}\\x+1=-\sqrt{\dfrac{3}{2}}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-2-\sqrt{6}}{2}\\x=\dfrac{-2+\sqrt{6}}{2}\end{matrix}\right.\)
\(b,\left(x-2\right)\left(x+2\right)-\left(x+3\right)^2-2x-5=0\\ \Leftrightarrow x^2-4-x^2-6x-9-2x-5=0\\ \Leftrightarrow-8x=18\\ \Leftrightarrow x=-\dfrac{9}{4}\)
LR
2
21 tháng 3 2021
Ta có: \(\left(1-x\right)^2+\left(x-x^2\right)+3=0\)
\(\Leftrightarrow x^2-2x+1+x-x^2+3=0\)
\(\Leftrightarrow4-x=0\)
hay x=4
Vậy: S={4}
21 tháng 3 2021
$⇔x^2-2x+1+x-x^2+3=0$
$⇔-x=-4$
$⇔x=4$
Vậy phương trình đã cho có tập nghiệm S={4}
DL
2
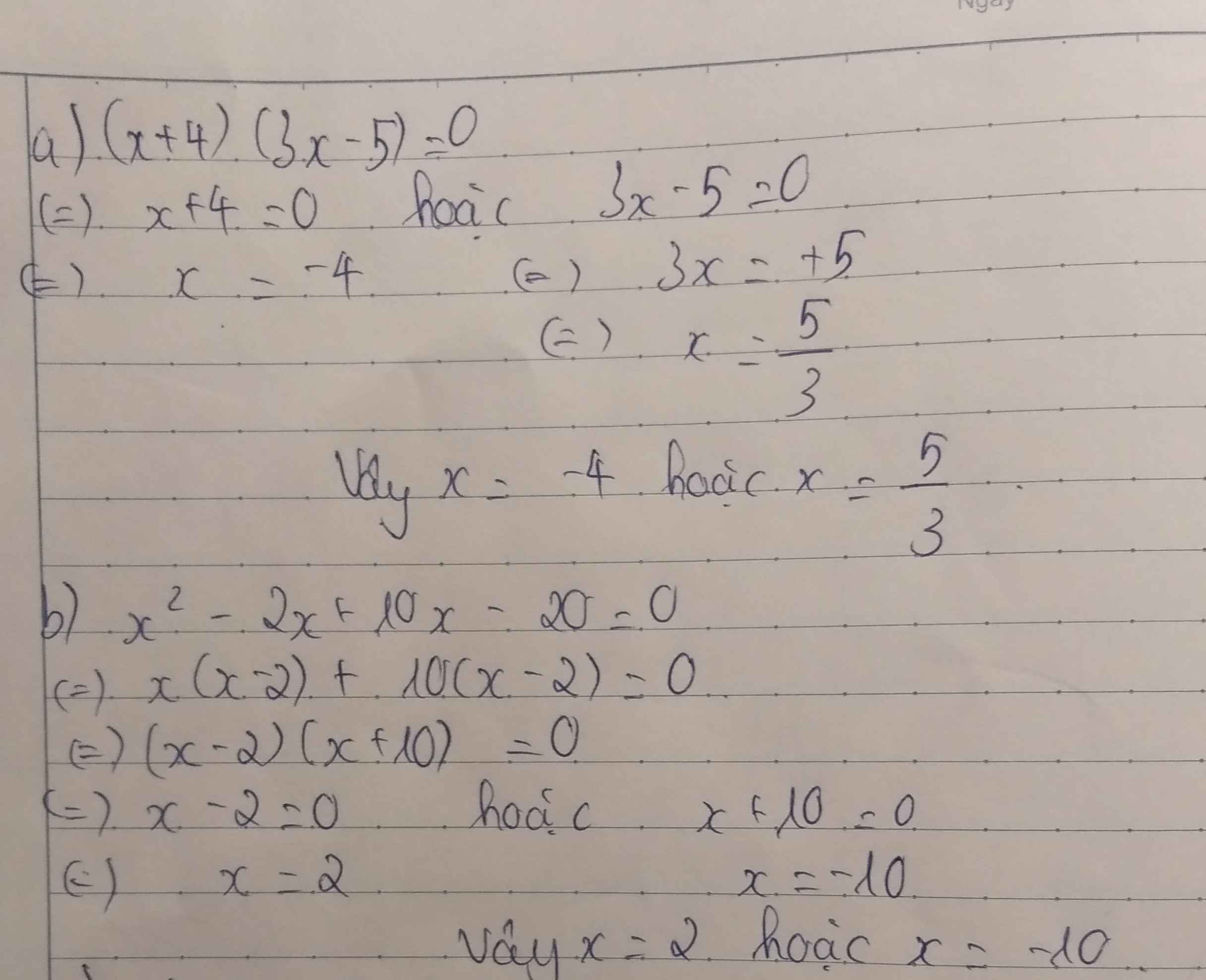
\(x^3+2x^2+3x=0\)\(\Leftrightarrow x.\frac{x^3+2x^2+3x}{x}=0\)
\(\Leftrightarrow x\left(x^2+2x+3\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x=0\\x^2+2x+3=0\end{cases}}\)
Ta sẽ c/m \(x^2+2x+3=0\) vô nghiệm.Thật vậy:
\(x^2+2x+3=\left(x+1\right)^2+2\ge2\forall x\)
Từ đó suy ra \(x^2+2x+3=0\) vô nghiệm.
Vậy : x = 0
\(\left(x+2\right)\left(2x-1\right)+1=4x^2\)
\(2x^2-x+4x-2+1=4x^2\)
\(\Rightarrow2x^2-3x+1=0\)
\(2x\left(x-1\right)-\left(x-1\right)=0\)
\(\left(x-1\right)\left(2x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\2x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=\frac{1}{2}\end{cases}}}\)
Vậy \(\orbr{\begin{cases}x=1\\x=\frac{1}{2}\end{cases}}\)
ý còn lại tham khảo bài tth