MM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LL
2
S
29 tháng 12 2023
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}\)(ĐK: \(x\ne0\))
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}\)
\(\Rightarrow\left(1+2y\right)24=\left(1+4y\right)18\)
\(\Rightarrow24+48y=18+72y\)
\(\Rightarrow72y-48y=24-18\)
\(\Rightarrow24y=6\)
\(\Rightarrow y=\dfrac{1}{4}\) \(\left(1\right)\)
Ta có: \(\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}\) \(\left(2\right)\)
Thay \(\left(1\right)\) vào \(\left(2\right)\), ta có:
\(\dfrac{1+4\cdot\dfrac{1}{4}}{24}=\dfrac{1+6\cdot\dfrac{1}{4}}{6x}\)
\(\Rightarrow\dfrac{2}{24}=\dfrac{\dfrac{5}{2}}{6x}\)
\(\Rightarrow6x=\dfrac{\dfrac{5}{2}\cdot24}{2}\)
\(\Rightarrow6x=30\)
\(\Rightarrow x=5\)(thỏa mãn)
Vậy x = 5 và y = \(\dfrac{1}{4}\)
#YM
CD
3
S
10 tháng 10 2017
Ta có:\(\frac{1+2y}{18}=\frac{1+4y}{24}=\frac{1+6y}{6x}=\frac{2\left(1+2y\right)-\left(1+4y\right)}{2.18-24}=\frac{1+2y+1+4y-\left(1+6y\right)}{18+24-6x}\)
\(\Rightarrow\frac{1}{6}=\frac{1}{6x}\Rightarrow x=1\)
MH
18 tháng 9 2021
2) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{1+2y}{18}=\dfrac{1+6y}{6x}=\dfrac{1+2y+1+6y}{18+6x}=\dfrac{2\left(1+4y\right)}{2\left(9+3x\right)}=\dfrac{1+4y}{9+3x}\)
⇒ \(\dfrac{1+4y}{9+3x}=\dfrac{1+4y}{28}\)
⇒\(9+3x=28\)
⇒\(3x=19\)
⇒\(x=\dfrac{19}{3}\)
bạn thay vào là tìm được y
DT
1
T
11 tháng 8 2018
Áp dụng tính chất dãy tỉ số bằng nhau,ta có:
\(\dfrac{1+2y}{18}=\dfrac{1+6y}{6x}\Rightarrow\dfrac{1+2y+1+6y}{18+6x}\Rightarrow\dfrac{8y+2}{18+6x}\Leftrightarrow\dfrac{2\left(1+4y\right)}{2\left(9+3x\right)}=\dfrac{1+4y}{9+3x}\)
\(\Rightarrow\dfrac{1+4y}{9+3x}=\dfrac{1+4y}{24}\Leftrightarrow9+3x=24\Rightarrow x=\dfrac{24-9}{3}=5\)
Thay x=5 vào biểu thức: \(\dfrac{1+2y}{18}=\dfrac{1+6y}{6x}\),ta đc:
\(\dfrac{1+2y}{18}=\dfrac{1+6y}{6.5}\Leftrightarrow\dfrac{1+2y}{18}=\dfrac{1+6y}{30}\Leftrightarrow\dfrac{5\left(1+2y\right)}{90}=\dfrac{3\left(1+6y\right)}{90}\)
\(\Leftrightarrow5\left(1+2y\right)=3\left(1+6y\right)\Leftrightarrow5+10y=3+18y\)
\(\Leftrightarrow10y-18y=3-5\Leftrightarrow-8y=-2\Leftrightarrow y=\dfrac{1}{4}=0,25\)
vậy x=5 và y=0,25
DS
3
NT
30 tháng 12 2017
\(\dfrac{1+2y}{18}=\dfrac{1+6y}{6x}\\ \Rightarrow\dfrac{1+2y}{18}=\dfrac{1+6y}{6x}=\dfrac{\left(1+2y\right)+\left(1+6y\right)}{18+6x}\\ =\dfrac{2+8y}{18+6x}=\dfrac{1+4y}{9+3x}\\ \Rightarrow9+3x=24\\ \Rightarrow3x=15\\ \Rightarrow x=5\)
ND
1
NL
1
26 tháng 9 2018
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}=\dfrac{1+2y+1+6y}{18+6x}=\dfrac{2.\left(1+4y\right)}{2.\left(9+3x\right)}=\dfrac{1+4y}{9+3x}\)
⇒\(\dfrac{1+4y}{9+3x}=\dfrac{1+4y}{24}\)
⇒\(9+3x=24\)
⇒\(3x=24-9=15\)
⇒\(x=15:3=5\)
NT
2
2 tháng 9 2017
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}=\dfrac{1+2y+1+4y+1+6y}{18+24+6x}=\dfrac{3+12y}{6\left(7+x\right)}=\dfrac{3\left(1+4y\right)}{2.3\left(7+x\right)}=\dfrac{1+4y}{2\left(7+x\right)}=\dfrac{1+4y}{24}\)=> 7 + x = 12
=> x = 5
2 tháng 9 2017
Ta có :
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}\)
\(\Leftrightarrow24\left(1+2y\right)=18\left(1+4y\right)\)
\(\Leftrightarrow24+48y=18+72y\)
\(\Leftrightarrow24-18=72y-48y\)
\(\Leftrightarrow24y=6\)
\(\Leftrightarrow y=\dfrac{1}{4}\)
Thay \(y=\dfrac{1}{4}\) ta có :
\(\dfrac{1+1}{24}=\dfrac{1+\dfrac{3}{2}}{6x}\)
\(=\dfrac{1}{12}=\dfrac{\dfrac{5}{2}}{6x}\)
\(\Leftrightarrow6x=\dfrac{5}{2}.12\)
\(\Leftrightarrow6x=30\)
\(\Leftrightarrow x=5\)
Vạy ...
NT
2
2 tháng 9 2017
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}\)(1)
Từ \(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}\)=>\(24+48y=18+72y\)
=>24y=6=>\(y=\dfrac{1}{4}\)
Thay vào(1),ta có:
\(\dfrac{1+1}{24}=\dfrac{1+\dfrac{3}{2}}{6x}\)
=>\(\dfrac{2}{24}=\dfrac{\dfrac{5}{2}}{6x}\)
=>12x=60=>x=5
Vậy...
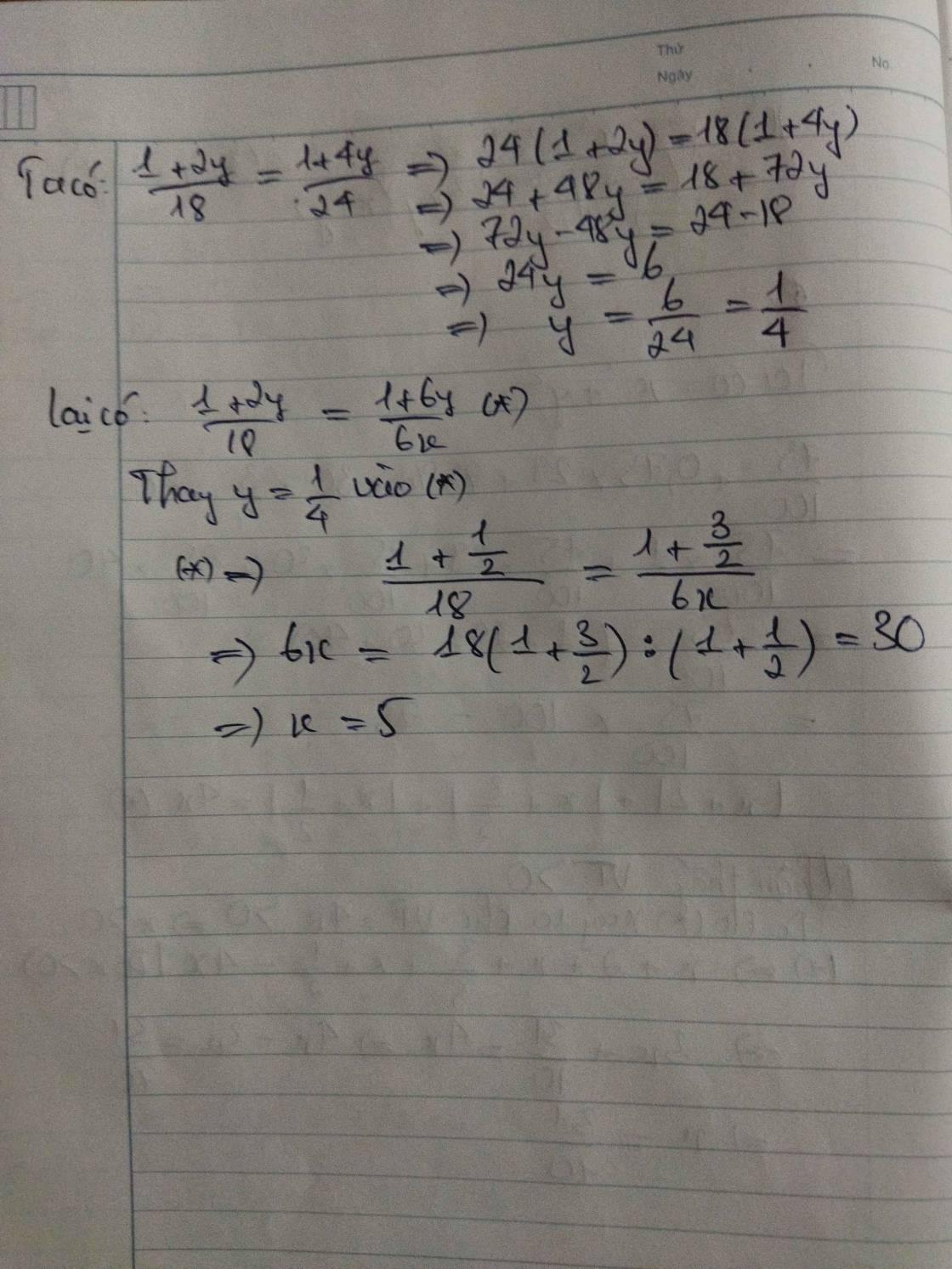
\(\dfrac{1+2y}{18}=\dfrac{1+4y}{24}\)
khi và chỉ khi: \(\left(1+2y\right).24=\left(1+4y\right).18\) \(\Rightarrow24+48y=18+72y\)\(\Rightarrow72y-48y=24-18\)
\(\Rightarrow24y=6\) \(\Rightarrow y=\dfrac{1}{4}\) Lại có: \(\dfrac{1+4y}{24}=\dfrac{1+6y}{6x}\) \(\Rightarrow\dfrac{1+4\cdot\dfrac{1}{4}}{24}=\dfrac{1+6\cdot\dfrac{1}{4}}{6x}\) \(\Rightarrow\dfrac{1}{12}=\dfrac{\dfrac{5}{2}}{6x}\) \(\Rightarrow6x.1=12\cdot\dfrac{5}{2}\) \(\Rightarrow x=30:6=5\) Vậy x=5;y=\(\dfrac{1}{4}\)