NV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
11 tháng 8 2018
Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
16 tháng 7 2015
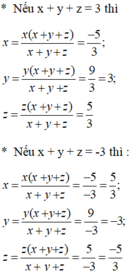
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
HL
1
3 tháng 5 2016
Theo tính chất dãy tỉ số bằng nhau.
Ta có x/2=y/3=z/5 và x+y+z=810
x/2=y/3=z/5=x+y+z=810/2*3*5=810/30=27
Do đó x/2=27 => x=27*2=54
y/3=27 => y=27*3=81
z/5=27 => z=27*5=135
20 tháng 10 2018
\(\left(x-5\right)^8+|y^2-4|=0\)
Vì \(\left(x-5\right)^8\ge0\)\(\forall x\)
\(|y^2-4|\ge0\)\(\forall y\)
\(\Rightarrow\left(x-5\right)^8+|y^2-4|\ge0\)\(\forall x,y\)
mà \(\left(x-5\right)^8+|y^2-4|=0\left(gt\right)\)
\(\Rightarrow\left(x-5\right)^8+|y^2-4|=0\Leftrightarrow\left(x-5\right)^8=0\)và \(|y^2-4|=0\)
\(\Leftrightarrow x-5=0\)và \(y^2-4=0\)
\(\Leftrightarrow x=5\)và \(y^2=4\)
\(\Leftrightarrow x=5\)và \(y=-2\)hoặc \(y=2\)
Vậy x = 5 , y = -2 hoặc y = 2
N
0
PT
1
CM
13 tháng 7 2019
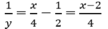
Suy ra y.(x - 2) = 4. Vì x, y ∈ Z nên x - 2 ∈ Z, ta có bảng sau:
Ta có: y và (x – 2) là ước của 4 và y.(x - 2) = 4.
| y | 1 | -1 | 2 | -2 | 4 | -4 |
| x - 2 | 4 | -4 | 2 | -2 | 1 | -1 |
| x | 6 | -2 | 4 | 0 | 3 | 1 |
N
1
H9
HT.Phong (9A5)
CTVHS
18 tháng 11 2023
x và y là hai đại lượng tỉ lệ thuận nên:
\(\Rightarrow y=kx\) (với k là hệ số tỉ lệ)
Ta có: \(x=15;y=20\)
\(\Rightarrow k=\dfrac{y}{x}=\dfrac{20}{15}=\dfrac{4}{3}\)
Vậy x và y là hai đại lượng tỉ lệ thuận, với x = 15 và y = 20 thì hệ số tỉ lệ (k) của y đối với x là \(\dfrac{4}{3}\)
Ta có \(\left|x-2011\right|+\left|x-2015\right|=\left|-x+2011\right|+\left|x-2015\right|\ge4\),\(\hept{\begin{cases}\left|x-2013\right|\ge0\\\left|y-2017\right|\ge0\end{cases}}\)
\(\Rightarrow VT\ge4\). Dấu = xảy ra khi \(\hept{\begin{cases}\left(-x+2011\right).\left(x-2015\right)\ge0\\x-2013=0\\y-2017=0\end{cases}\Rightarrow\hept{\begin{cases}x=2013\\y=2017\end{cases}}}\)
Vậy ...