K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
3
LT
26 tháng 2 2020
a) x=0 hoặc x+7=0
suy ra x=0 hoặc x=-7
b) x+12=0 hoặc x-3=0
x=-12 hoặc x=3
c) x=0 hoặc x+2=0 hoặc 7-x=0
x=0 hoặc x=-2 hoặc x=7
d) x-1=0 hoặc x+2=0 hoặc -x-3=0
suy ra x=1 hoặc x=-2 hoặc x=-3
22 tháng 3 2020
Bài làm
x( x + 7 ) = 0
<=> x = 0 hoẵ x + 7 = 0
=> x = 0 hoặc x = -7
Vậy x = 0 hoặc x = -7
( x + 12 )( x - 3 ) = 0
<=> x + 12 = 0 hoặc x - 3 = 0
=> x = -12 hoặc x = 3
Vậy x = -12 hoặc x = 3
( -x + 5 )( 3 - x ) = 0
<=> -x + 5 = 0 hoặc 3 - x = 0
=> x = 5 hoặc x = 3
Vậy x = 5 hoặc x = 3
x( 2 + x )( 7 - x ) = 0
<=> x = 0 hoặc 2 + x = 0 hoặc 7 - x = 0
=> x = 0 hoặc x = -2 hoặc x = 7
Vậy x = 0 hoặc x = -2 hoặc x j 7
( x - 1 )( x + 2 )( -x - 3 ) = 0
<=> ( x - 1 ) = 0 hoặc x + 2 = 0 hoặc ( -x - 3 ) = 0
<=> x = 1 hoăc x = -2 hoặc x = ( -3)
Vậy x = 1 hoặc x = 2 hoặc x = -3
TT
5
TD
5 tháng 2 2017
1/ ( x+12)(3-x)=0
=> \(\orbr{\begin{cases}x+12=0\\3-x=0\end{cases}}\)
=>\(\orbr{\begin{cases}x=-12\\x=3\end{cases}}\)
DL
5
NK
8 tháng 2 2016
Làm theo công thức: tích bằng 0 thì một trong x thừa số bằng 0 rồi xét các trường hợp
1 tháng 2 2017
\(1,x.\left(x+7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x+7=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-7\end{cases}}}\)
\(2,\left(x+12\right).\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+12=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-12\\x=3\end{cases}}}\)
\(3,\left(-x+5\right).\left(3-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}-x+5=0\\3-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\x=3\end{cases}}}\)
2 tháng 2 2021
4/ \(x.\left(2+x\right).\left(7-x\right)=0\)
\(\hept{\begin{cases}x=0\\2+x=0\\7-x=0\end{cases}}\) => \(\hept{\begin{cases}x=0\\x=-2\\x=7\end{cases}}\)
Vậy \(x=\left\{0,-2,7\right\}\)
5/ \(\left(x-1\right).\left(x+2\right).\left(-x-3\right)=0\)
\(\hept{\begin{cases}x-1=0\\x+2=0\\-x-3=0\end{cases}}\)=> \(\hept{\begin{cases}x=1\\x=-2\\x=-3\end{cases}}\)
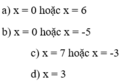
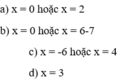
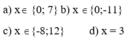
x-3=0
x=3
x - 3 = 0
x = 0 + 3
x = 3
Vậy x = 3