TM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
2
D
29 tháng 6 2018
\(\frac{x+32}{11}+\frac{x+33}{12}=\frac{x+34}{13}+\frac{x+35}{14}\)
\(\Leftrightarrow\left(\frac{x+32}{11}-1\right)+\left(\frac{x+33}{12}-1\right)=\left(\frac{x+34}{13}-1\right)+\left(\frac{x+35}{14}-1\right)\)
\(\Leftrightarrow\frac{x-21}{11}+\frac{x-21}{12}=\frac{x-21}{13}+\frac{x-21}{14}\)
\(\Leftrightarrow\left(x-21\right)\left(\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\right)=0\)
Vì \(\left(\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\right)\ne0\)
\(\Rightarrow x-21=0\Rightarrow x=21\)
29 tháng 6 2018
\(\frac{x+32}{11}+\frac{x+33}{12}=\frac{x+34}{13}+\frac{x+35}{14}\)
\(\Leftrightarrow\left(\frac{x+32}{11}-1\right)+\left(\frac{x+33}{12}-1\right)=\left(\frac{x+34}{13}-1\right)+\left(\frac{x+35}{14}-1\right)\)( trừ cả hai vế cho 2 )
\(\Leftrightarrow\frac{x-21}{11}+\frac{x-21}{12}=\frac{x-21}{13}+\frac{x-21}{14}\)
\(\Leftrightarrow\frac{x-21}{11}+\frac{x-21}{12}-\frac{x-21}{13}-\frac{x-21}{14}=0\)
\(\Leftrightarrow\left(x-21\right)\left(\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\right)=0\)
Mà \(\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\ne0\)
\(\Rightarrow x-21=0\)
\(\Leftrightarrow x=21\)
Vậy \(x=21\)
NK
4
12 tháng 2 2020
(x-99) (1/30 + 1/32 + 1/34 - 1/36 - 1/38) = 0
SUy ra x - 99 = 0
VẬy x =99
H9
HT.Phong (9A5)
CTVHS
22 tháng 6 2023
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
S
1
1 tháng 11 2020
\(\left|x+\frac{3}{4}\right|-\frac{1}{3}=0\)
\(\left|x+\frac{3}{4}\right|=\frac{1}{3}\)
\(\Rightarrow x+\frac{3}{4}=\pm\frac{1}{3}\)
\(\cdot x+\frac{3}{4}=\frac{1}{3}\)
\(x=-\frac{5}{12}\)
\(\cdot x+\frac{3}{4}=-\frac{1}{3}\)
\(x=-\frac{13}{12}\)
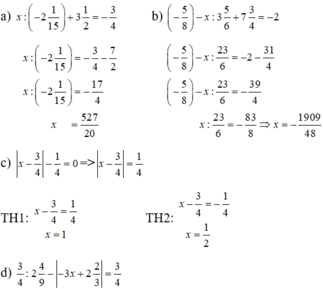
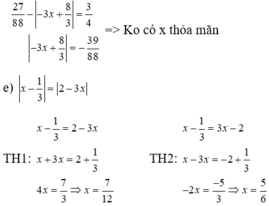
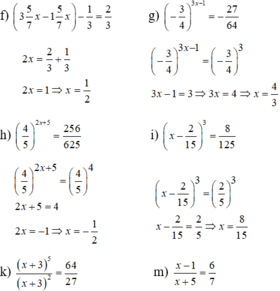
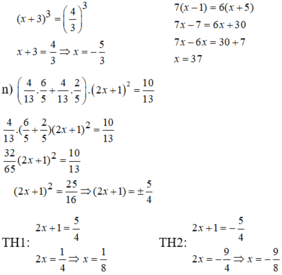
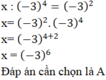
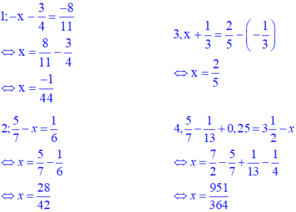
`Answer:`
`\frac{x-1}{34}+\frac{x-2}{34}=\frac{x-3}{32}+\frac{x-4}{31}`
`<=>\frac{x-1}{34}-1+\frac{x-2}{33}-1=\frac{x-3}{32}-1+\frac{x-4}{31}-1`
`<=>\frac{x-35}{34}+\frac{x-35}{33}=\frac{x-35}{32}+\frac{x-35}{31}`
`<=>(x-35)(\frac{1}{34}+\frac{1}{33}-\frac{1}{32}-\frac{1}{31})=0`
`<=>x-35=0`
`<=>x=35`