Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một. Khai triển vế trái của phương trình:
(x-3)(x+3) = x(x+3) - 3(x+3) = x^2 + 3x - 3x - 9 = x^2 - 9
Khai triển vế phải của phương trình:
(x-5)^2 = (x-5)(x-5) = x(x-5) - 5(x-5) = x^2 - 5x - 5x + 25 = x^2 - 10x + 25
Đặt hai cạnh bằng nhau:
x^2 - 9 = x^2 - 10x + 25
Trừ x^2 từ cả hai phía:
-9 = -10x + 25
Trừ 25 từ cả hai vế:
-34 = -10 lần
Chia cả hai vế cho -10:
x = 3,4
b. Khai triển vế trái của phương trình:
(2x+1)^2 - 4x(x-1) = (2x+1)(2x+1) - 4x^2 + 4x = 4x^2 + 2x + 2x + 1 - 4x^2 + 4x = 8x + 1
Đặt vế trái bằng 17:
8x + 1 = 17
Trừ 1 cho cả hai vế:
8x = 16
Chia cả hai vế cho 8:
x = 2
c. Khai triển vế trái của phương trình:
(3x-2)(3x+2) - 9(x-1)x = (9x^2 - 4) - 9x^2 + 9x - 9x = -4 + 9x
Đặt vế trái bằng 0:
-4 + 9x = 0
Thêm 4 vào cả hai bên:
9x = 4
Chia cả hai vế cho 9:
x = 4/9
d. Khai triển vế trái của phương trình:
(3-x)^3 - (x+3)^3 = (27 - 9x + x^2) - (x^3 + 9x^2 + 27) = 27 - 9x + x^2 - x^3 - 9x^2 - 27 = -x^3 - 8x^2 - 9x
Đặt vế trái bằng 36x^2 - 54x:
-x^3 - 8x^2 - 9x = 36x^2 - 54x
Cộng x^3 + 8x^2 + 9x vào cả hai vế:
0 = 37x^2 - 63x
Chia cả hai vế cho x:
0 = 37x - 63
Thêm 63 vào cả hai bên:
63 = 37 lần
Chia cả hai vế cho 37:
x = 63/37

a: Ta có: \(\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x-5\right)=-4\)
\(\Leftrightarrow x^2+5x+6-x^2+7x-10=-4\)
\(\Leftrightarrow12x=0\)
hay x=0
b: Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-x\left(x-3\right)\left(x+3\right)=8\)
\(\Leftrightarrow x^3+1-x^3+9x=8\)
\(\Leftrightarrow9x=7\)
hay \(x=\dfrac{7}{9}\)
c: Ta có: \(4x^2-9=\left(3x+1\right)\left(2x-3\right)\)
\(\Leftrightarrow\left(3x+1\right)\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(3x+1-2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\end{matrix}\right.\)

a) Ta có: \(x^4-16x^2=0\)
\(\Leftrightarrow x^2\left(x^2-16\right)=0\)
\(\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
b) Ta có: \(x^8+36x^4=0\)
\(\Leftrightarrow x^4\left(x^4+36\right)=0\)
\(\Leftrightarrow x^4=0\)
hay x=0
c) Ta có: \(\left(x-5\right)^3-x+5=0\)
\(\Leftrightarrow\left(x-5\right)\cdot\left[\left(x-5\right)^2-1\right]=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\\x=6\end{matrix}\right.\)
d) Ta có: \(5\left(x-2\right)-x^2+4=0\)
\(\Leftrightarrow5\left(x-2\right)-\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(5-x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

a) (2x - 5)2 - (5 + 2x) = 0
<=> 4x2 - 22x + 20 = 0
\(\Leftrightarrow\left(2x-\dfrac{11}{2}\right)^2=\dfrac{41}{4}\)
\(\Leftrightarrow x=\dfrac{\pm\sqrt{41}+11}{4}\)
b) \(27x^3-54x^2+36x=0\)
\(\Leftrightarrow x\left(3x^2-6x+4\right)=0\)
\(\Leftrightarrow x=0\) (Vì \(3x^2-6x+4=3\left(x-1\right)^2+1>0\forall x\))
c) x3 + 8 - (x + 2).(x - 4) = 0
\(\Leftrightarrow\left(x+2\right).\left(x^2-2x+4\right)-\left(x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-3x+8\right)=0\)
\(\Leftrightarrow x=-2\) (Vì \(x^2-3x+8=\left(x-\dfrac{3}{2}\right)^2+\dfrac{23}{4}>0\))
d) \(x^6-1=0\)
\(\Leftrightarrow\left(x^2\right)^3-1=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\)
\(\Leftrightarrow x^2-1=0\) (Vì \(x^4+x^2+1>0\))
\(\Leftrightarrow x=\pm1\)
\(d,x^6-1=0\\ \Leftrightarrow\left(x^2\right)^3-1^3=0\\ \Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x^4+x^2+1=0\left(Vô.lí,vì:x^4\ge0;x^2\ge0,\forall x\in R\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ c,\left(x^3+8\right)-\left(x+2\right)\left(x-4\right)=0\\ \Leftrightarrow\left(x^3+8\right)-\left(x^2-2x-8\right)=0\\ \Leftrightarrow x^3-x^2+2x+16=0\\ \Leftrightarrow x^3+2x^2-3x^2-6x+8x+16=0\\ \Leftrightarrow x^2\left(x+2\right)-3x\left(x+2\right)+8\left(x+2\right)=0\\ \Leftrightarrow\left(x^2-3x+8\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-3x+8=0\left(Vô.lí\right)\\x+2=0\end{matrix}\right.\Leftrightarrow x=-2\)

\(a,\Leftrightarrow\left(3x-1\right)\left(3x+1\right)-3\left(3x-1\right)=0\\ \Leftrightarrow\left(3x-1\right)\left(3x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-2\right)^2\left(x-1\right)^2-\left(x-2\right)^2-\left(x-2\right)^3=0\\ \Leftrightarrow\left(x-2\right)^2\left[\left(x-1\right)^2-1-\left(x-2\right)\right]=0\\ \Leftrightarrow\left(x-2\right)^2\left(x^2-2x+1-1-x+2\right)=0\\ \Leftrightarrow\left(x-2\right)^2\left(x^2-3x+2\right)=0\\ \Leftrightarrow\left(x-2\right)^3\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)

1: =>(x+3)(x-5)=0
=>x=5 hoặc x=-3
2: =>(x-1)(5x-1)=0
=>x=1/5 hoặc x=1
5: =>(x-4)*x=0
=>x=0 hoặc x=4
10: =>(x+5)(x-3)=0
=>x=3 hoặc x=-5
9: =>(x-2)(x-4)=0
=>x=2 hoặc x=4
7: =>(x-6)(2x-1)=0
=>x=1/2 hoặc x=6
8: =>(2x-1)(3x-12)=0
=>x=4 hoặc x=1/2

a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)
\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)
\(\Leftrightarrow-10x^2-10x=0\)
\(\Leftrightarrow-10x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
c: Ta có: \(x^3+3x^2+3x+28=0\)
\(\Leftrightarrow\left(x+1\right)^3=-27\)
\(\Leftrightarrow x+1=-3\)
hay x=-4

a) \(4x^3-36x=0\)
\(\Leftrightarrow4x\left(x^2-9\right)=0\)
\(\Leftrightarrow4x\left(x+3\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=0\\x+3=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=3\end{matrix}\right.\)
b) \(\left(x-2\right)^2-4x+8=0\)
\(\Leftrightarrow\left(x-2\right)^2-\left(4x-8\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2-4\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2-4\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)
c) \(x^3+\left(x+3\right)\left(x-9\right)=-27\)
\(\Leftrightarrow\left(x^3+27\right)+\left(x+3\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9+x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-2x\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=2\end{matrix}\right.\)

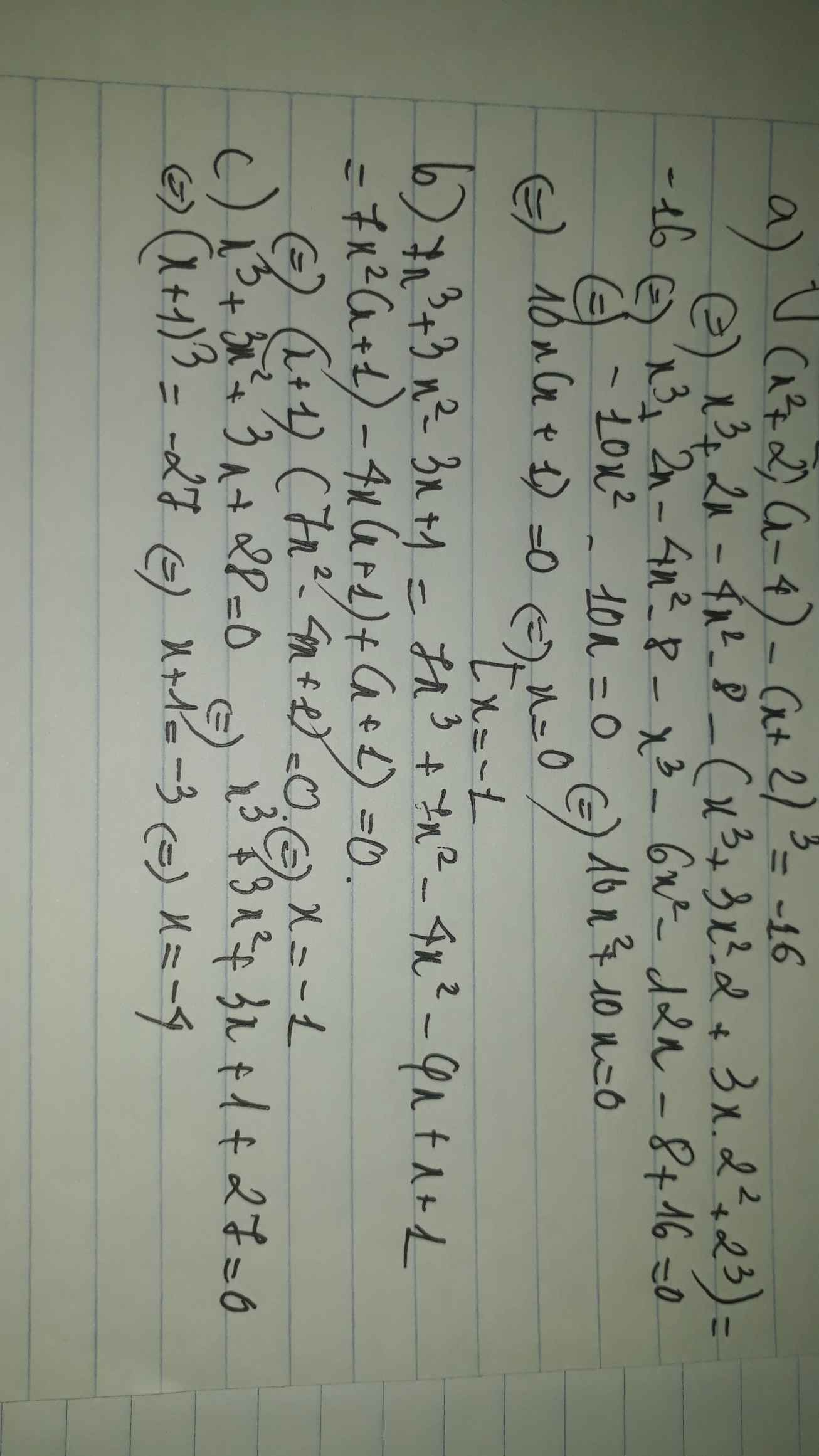
Biến đổi ta được:
a) x = 0. b) x = 2 3 .