LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 3 2021
a) \(Ư\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Suy ra \(x\in\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
b) \(Ư\left(13\right)=\left\{\pm1;\pm13\right\}\)
| x + 1 | 1 | 13 | -1 | -13 |
| x | 0 | 12 | -2 | -14 |
Suy ra \(x\in\left\{0;12;-2;-14\right\}\)
c) Số nào chia hết cho x - 3 vậy????
d) \(\left(x+8\right)⋮\left(x+2\right)\Leftrightarrow\left(x+2+6\right)⋮\left(x+2\right)\)
Mà x + 2 chia hết cho x + 2 nên 6 chia hết cho x + 2
\(Ư\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| x + 2 | 1 | 2 | 3 | 6 | -1 | -2 | -3 | -6 |
| x | -1 | 0 | 1 | 4 | -3 | -4 | -5 | -8 |
Suy ra \(x\in\left\{-1;0;1;4;-3;-4;-5;-8\right\}\)
ND
Nguyễn Đức Trí
VIP
3 tháng 9 2023
1) \(2⋮x\Rightarrow x\in U\left(2\right)=\left\{1;2\right\}\left(x\inℕ\right)\)
2) \(2⋮\left(x+1\right)\Rightarrow x+1\in U\left(2\right)=\left\{1;2\right\}\Rightarrow x\in\left\{0;1\right\}\left(x\inℕ\right)\)
3) \(2⋮\left(x+2\right)\Rightarrow x+2\in U\left(2\right)=\left\{1;2\right\}\Rightarrow x\in\left\{-1;0\right\}\Rightarrow x\in\left\{0\right\}\left(x\inℕ\right)\)
4) \(2⋮\left(x-1\right)\Rightarrow x-1\in U\left(2\right)=\left\{1;2\right\}\Rightarrow x\in\left\{2;3\right\}\left(x\inℕ\right)\)
SD
3 tháng 9 2023
1. 2 chia hết cho x
Ta có 2 là số chẵn, nên x phải là số chẵn. Vậy các số tự nhiên x thỏa mãn là x = 2, 4, 6, …
2. 2 chia hết cho (x + 1)
Ta có 2 chia hết cho (x + 1) khi và chỉ khi x + 1 là số chẵn. Điều này tương đương với x là số lẻ. Vậy các số tự nhiên x thỏa mãn là x = 1, 3, 5, …
3. 2 chia hết cho (x + 2)
Ta có 2 chia hết cho (x + 2) khi và chỉ khi x + 2 là số chẵn. Điều này tương đương với x là số chẵn. Vậy các số tự nhiên x thỏa mãn là x = 0, 2, 4, …
4. 2 chia hết cho (x - 1)
Ta có 2 chia hết cho (x - 1) khi và chỉ khi x - 1 là số chẵn. Điều này tương đương với x là số lẻ. Vậy các số tự nhiên x thỏa mãn là x = 3, 5, 7, …
MN
3
29 tháng 10 2018
Theo bài ra, ta có: \(\left(x-1\right)\in BC\left(5;6;8\right)\)
5 = 5
6 = 2.3
8 = 23
\(BCNN\left(5;6;8\right)=2^3.3.5=120\)
Vậy \(\left(x-1\right)\in BC\left(120\right)=\left\{120;240;...;720;840;960;...\right\}\)
Mà \(800< x< 900\Rightarrow799< x-1< 899\)
Do đó: \(x-1=840\)
Vậy x = 841
29 tháng 10 2018
ta có:
\(x-1⋮5\Rightarrow x-1\in B\left(5\right)\)
\(x-1⋮6\Rightarrow x-1\in B\left(6\right)\)
\(x-1⋮8\Rightarrow x-1\in B\left(8\right)\)
\(\Rightarrow x-1\in BC\left(5;6;8\right)\)
Phân tích ra thừa số nguyên tố
5 = 5
6 = 2.3
8 = 23
\(\Rightarrow BCNN\left(5;6;8\right)=2^3.3.5=120\)
\(\Rightarrow x-1\in B\left(120\right)=\left\{120;240;360;480;600;720;840;960;...\right\}\)
mà \(800< x< 900\Rightarrow799< x-1< 899\)
\(\Rightarrow x-1=840\)
\(x=840+1=841\)
23 tháng 11 2021
\(\Leftrightarrow x\in BC\left(15,20\right)=B\left(60\right)=\left\{0;60;120;...\right\}\text{ và }50< x< 70\\ \Leftrightarrow x=60\)
HN
3
17 tháng 2 2021
19 chia hết cho x
x \(\in\) Ư( 19 )
x \(\in\) { 1 ; 19 }
17 tháng 2 2021
a) Ta có: \(19⋮x\)
\(\Leftrightarrow x\inƯ\left(19\right)\)
hay \(x\in\left\{1;-1;19;-19\right\}\)
Vậy: \(x\in\left\{1;-1;19;-19\right\}\)
b) Ta có: \(23⋮x+1\)
\(\Leftrightarrow x+1\inƯ\left(23\right)\)
\(\Leftrightarrow x+1\in\left\{1;-1;23;-23\right\}\)
hay \(x\in\left\{0;-2;22;-24\right\}\)
Vậy: \(x\in\left\{0;-2;22;-24\right\}\)
c) Ta có: \(12⋮x-1\)
\(\Leftrightarrow x-1\inƯ\left(12\right)\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
hay \(x\in\left\{2;0;3;-1;4;-2;5;-3;7;-5;13;-11\right\}\)
Vậy: \(x\in\left\{2;0;3;-1;4;-2;5;-3;7;-5;13;-11\right\}\)
PT
1
CM
22 tháng 4 2018
a) (x + 6) - x chia hết cho x => 6 chia hết cho x hay xÎƯ(6) = {-6; -3; -2; -l; l; 2; 3; 6}.
b) ( x +9) - (x + l) chia hết cho (x + l) =>8 chia hết cho (x + l)
=> x + 1 ÎƯ (8) = { - 8; -4; -2; -1; 1; 2; 4; 8}.
Từ đó tìm được x Î {- 9; - 5; - 3; - 2; 0; 1; 3; 7}.
c) (2 + l) -2 (x - l) chia hết cho (x - l) => 3 chia hết cho (x - l)
=> x - 1Î Ư (3) = {- 3; -1; 1; 3}. Từ đó tìm được x Î{ - 2; 0; 2; 4}.
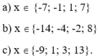
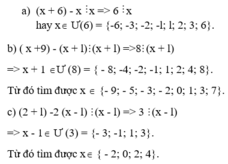
Để tìm x sao cho 756, 594 và 900 đều chia hết cho x, ta cần tìm ước chung lớn nhất của các số này.
Phân tích các số thành thừa số nguyên tố:
756 = 2² x 3³ x 7
594 = 2 x 3² x 11
900 = 2² x 3² x 5²
Ta thấy rằng ước chung lớn nhất của 756, 594 và 900 là 2² x 3² = 36.
Vậy x = 36.