Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,-\dfrac{x}{2}+\dfrac{2x}{3}+\dfrac{x+1}{4}+\dfrac{2x+1}{6}=\dfrac{8}{3}\)
\(\Rightarrow-\dfrac{6x}{12}+\dfrac{8x}{12}+\dfrac{3\left(x+1\right)}{12}+\dfrac{2\left(2x+1\right)}{12}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{-6x+8x+3x+3+4x+2}{12}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{9x+5}{12}=\dfrac{8}{3}\)
\(\Rightarrow27x+15=96\)
\(\Rightarrow27x=81\)
\(\Rightarrow x=3\left(tm\right)\)
\(b,\dfrac{3}{2x+1}+\dfrac{10}{4x+2}-\dfrac{6}{6x+3}=\dfrac{12}{26}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{10}{2\left(2x+1\right)}-\dfrac{6}{3\left(2x+1\right)}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{5}{2x+1}-\dfrac{2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3+5-2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{6}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow2x+1=13\)
\(\Rightarrow2x=12\)
\(\Rightarrow x=6\left(tm\right)\)
#Toru
a) \(-\dfrac{x}{2}+\dfrac{2x}{3}+\dfrac{x+1}{4}+\dfrac{2x+2}{6}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{-6x}{12}+\dfrac{8x}{12}+\dfrac{3\left(x+1\right)}{12}+\dfrac{2\left(2x+1\right)}{12}=\dfrac{4\cdot8}{12}\)
\(\Rightarrow-6x+8x+3x+3+4x+2=32\)
\(\Rightarrow9x+5=32\)
\(\Rightarrow9x=32-5\)
\(\Rightarrow9x=27\)
\(\Rightarrow x=\dfrac{27}{9}\)
\(\Rightarrow x=3\)
b) \(\dfrac{3}{2x+1}+\dfrac{10}{4x+2}-\dfrac{6}{6x+3}=\dfrac{12}{26}\) (ĐK: \(x\ne-\dfrac{1}{2}\))
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{10}{2\left(2x+1\right)}-\dfrac{6}{3\left(2x+1\right)}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{5}{2x+1}-\dfrac{2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{6}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow2x+1=13\)
\(\Rightarrow2x=12\)
\(\Rightarrow x=\dfrac{12}{2}\)
\(\Rightarrow x=6\left(tm\right)\)

a) 2ˣ + 2ˣ⁺³ = 72
2ˣ.(1 + 2³) = 72
2ˣ.9 = 72
2ˣ = 72 : 9
2ˣ = 8
2ˣ = 2³
x = 3
b) Để số đã cho là số nguyên thì (x - 2) ⋮ (x + 1)
Ta có:
x - 2 = x + 1 - 3
Để (x - 2) ⋮ (x + 1) thì 3 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(3) = {-3; -1; 1; 3}
⇒ x ∈ {-4; -2; 0; 2}
Vậy x ∈ {-4; -2; 0; 2} thì số đã cho là số nguyên
c) P = |2x + 7| + 2/5
Ta có:
|2x + 7| ≥ 0 với mọi x ∈ R
|2x + 7| + 2/5 ≥ 2/5 với mọi x ∈ R
Vậy GTNN của P là 2/5 khi x = -7/2

để \(\dfrac{x+1}{x-1}\)nguyên thì
(x+1)⋮(x-1)
=> (x+1)-(x-1)⋮(x-1)
=> (x+1-x+1)⋮(x-1)
=> 2⋮(x+1)
=> x+1 ∈Ư (2)={-2;-1;1;2}
ta có bảng sau
| x+1 | -2 | -1 | 1 | 2 |
| x | -3 | -2 | 0 |
1 |
vậy để \(\dfrac{x+1}{x-1}\)thì x ∈{-3;-2;0;1}

b, Ta có : \(\dfrac{x}{3}=\dfrac{y}{4};\dfrac{y}{5}=\dfrac{z}{6}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}\)
Đặt \(x=15k;y=20k;z=24k\)
Thay vào A ta được : \(A=\dfrac{30k+60k+96k}{45k+80k+120k}=\dfrac{186k}{245k}=\dfrac{186}{245}\)

a) \(A\left(x\right)=x^7-2x^6+2x^3-2x^4-x^7+x^5+2x^6-x+5+2x^4-x^5\)
\(A\left(x\right)=(x^7-x^7)+(-2x^6+2x^6)+2x^3+(-2x^4+2x^4)+(x^5-x^5)-x+5\)
\(A\left(x\right)=2x^3-x+5\)
- Bậc của đa thức A(x) là 3
- Hệ số tự do: 5
- Hệ số cao nhất: 2
b) \(B\left(x\right)=-3x^5+4x^4-2x+\dfrac{1}{2}-2x^4+3x-x^5-2x^4+\dfrac{5}{2}+x\)
\(B\left(x\right)=(-3x^5-x^5)+(4x^4-2x^4-2x^4)+(-2x+x+3x)+\left(\dfrac{1}{2}+\dfrac{5}{2}\right)\)
\(B\left(x\right)=-4x^5+2x+3\)
- Bậc của đa thức B(x) là 5
- Hệ số tự do: 3
- Hệ số cao nhất: \(-4\)
c) \(C\left(y\right)=5y^2-2.\left(y+1\right)+3y.\left(y^2-2\right)+5\)
\(C\left(y\right)=5y^2-2y-2+3y\left(y^2-2\right)+5\)
\(C\left(y\right)=5y^2-2y-2+3y^3-6y+5\)
\(C\left(y\right)=5y^2-2y+3+3y^3-6y\)
\(C\left(y\right)=5y^2-8y+3+3y^3\)
\(C\left(y\right)=3y^3+5y^2-8y+3\)
- Bậc của đa thức C(y) là 3
- Hệ số tự do: 3
- Hệ số cao nhất: 3

Dạng 1:
a) $4x+9=4x+\frac{9}{4}.4=4(x+\frac{9}{4}\Rightarrow$ Nghiệm là $-\frac{9}{4}$
b) $-5x+6=-5x+(-5).(-\frac{6}{5})=-5(x-\frac{6}{5})\Rightarrow$ Nghiệm là $\frac{6}{5}$
c) $7-2x=-2x+7=-2x+(-2).(-\frac{7}{2})=-2(x-\frac{7}{2})\Rightarrow$ Nghiệm là $\frac{7}{2}$
d) $2x+5=2x+2.\frac{5}{2}=2.(x+\frac{5}{2})\Rightarrow$ Nghiệm là $-\frac{5}{2}$
e) $2x+6=2x+2.3=2(x+3)\Rightarrow$ Nghiệm là -3
g) $3x-\frac{1}{4}=3x-3.(\frac{1}{12})=3(x-\frac{1}{12})\Rightarrow$ Nghiệm là $\frac{1}{12}$
h) $3x-9=3x-3.3=3(x-3)\Rightarrow$ Nghiệm là 3
k) $-3x-\frac{1}{2}=-3x-3.(\frac{1}{6})=-3(x+\frac{1}{6})\Rightarrow$ Nghiệm là $-\frac{1}{6}$
m) $-17x-34=-17x-17.2=-17(x+2)\Rightarrow$ Nghiệm là -2
n) $2x-1=2x+2.(-\frac{1}{2})=3(x-\frac{1}{2})\Rightarrow$ Nghiệm là $\frac{1}{2}$
q) $5-3x=-3x+5=-3x+(-3).(-\frac{5}{3})=-3(x-\frac{5}{3})\Rightarrow$ Nghiệm là $\frac{5}{3}$
p) $3x-6=3x+3.(-2)=3(x-2)\Rightarrow$ Nghiệm là 2

a) Ta có: \(\dfrac{4}{5}-3\left|x\right|=\dfrac{1}{5}\)
\(\Leftrightarrow3\left|x\right|=\dfrac{4}{5}-\dfrac{1}{5}=\dfrac{3}{5}\)
\(\Leftrightarrow\left|x\right|=\dfrac{1}{5}\)
hay \(x\in\left\{\dfrac{1}{5};-\dfrac{1}{5}\right\}\)
b) Ta có: \(4x-\dfrac{1}{2}x+\dfrac{3}{5}x=\dfrac{4}{5}\)
nên \(\dfrac{41}{10}x=\dfrac{4}{5}\)
hay \(x=\dfrac{8}{41}\)
c) Ta có: \(\left(2x-8\right)\left(10-5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-8=0\\10-5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=8\\5x=10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
d) Ta có: \(\dfrac{3}{4}+\dfrac{1}{4}\left|2x-1\right|=\dfrac{7}{2}\)
\(\Leftrightarrow\dfrac{1}{4}\left|2x-1\right|=\dfrac{7}{2}-\dfrac{3}{4}=\dfrac{14}{4}-\dfrac{3}{4}=\dfrac{11}{4}\)
\(\Leftrightarrow\left|2x-1\right|=11\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=11\\2x-1=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=12\\2x=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-5\end{matrix}\right.\)
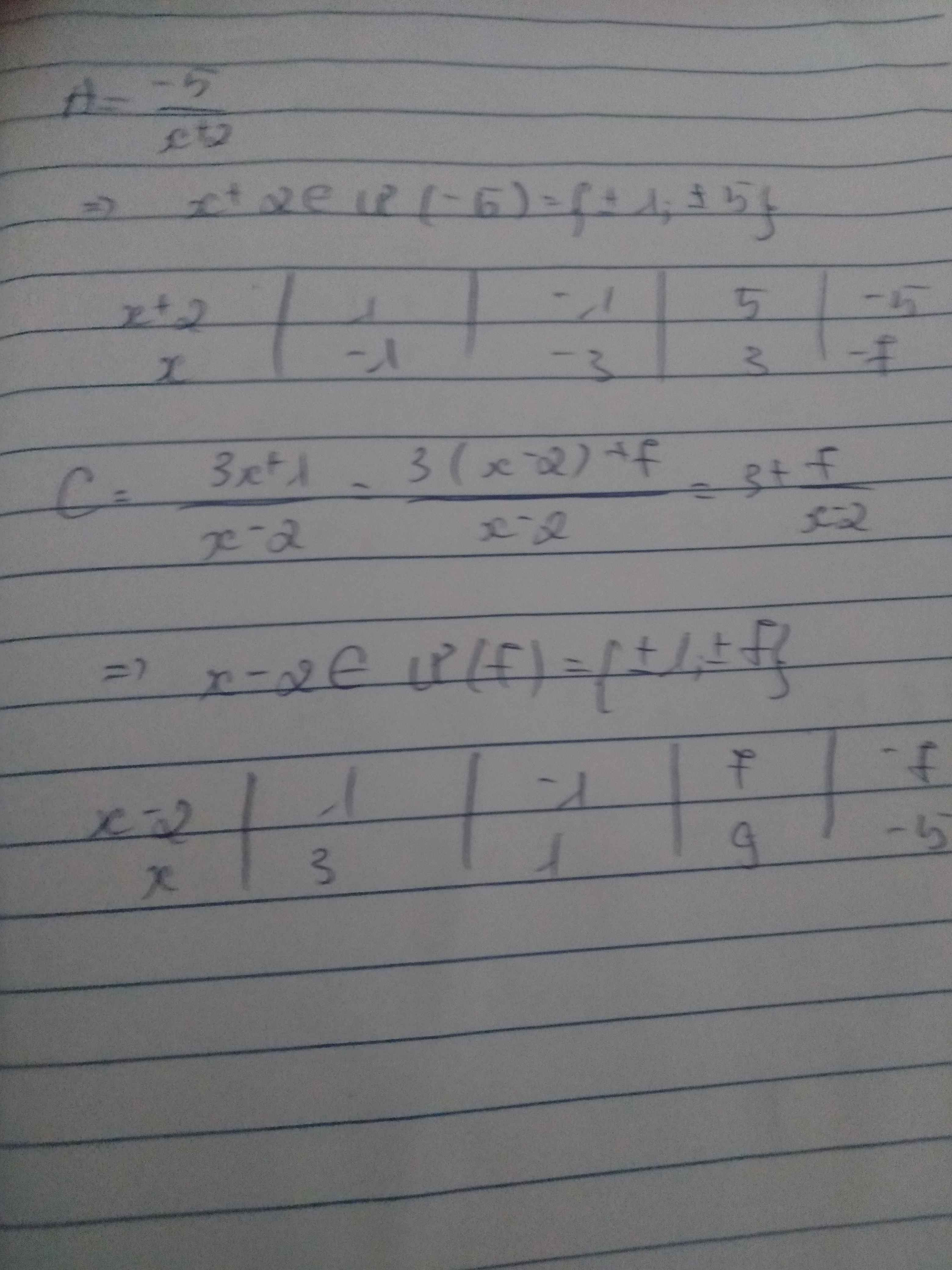
a) \(P=\dfrac{2x+5}{x+3}\inℤ\left(x\inℤ;x\ne-3\right)\)
\(\Rightarrow2x+5⋮x+3\)
\(\Rightarrow2x+5-2\left(x+3\right)⋮x+3\)
\(\Rightarrow2x+5-2x-6⋮x+3\)
\(\Rightarrow-1⋮x+3\)
\(\Rightarrow x+3\in\left\{-1;1\right\}\)
\(\Rightarrow x\in\left\{-4;-2\right\}\)
b) \(P=\dfrac{3x+4}{x+1}\inℤ\left(x\inℤ;x\ne-1\right)\)
\(\Rightarrow3x+4⋮x+1\)
\(\Rightarrow3x+4-3\left(x+1\right)⋮x+1\)
\(\Rightarrow3x+4-3x-3⋮x+1\)
\(\Rightarrow1⋮x+1\)
\(\Rightarrow x+1\in\left\{-1;1\right\}\)
\(\Rightarrow x\in\left\{-2;0\right\}\)
c) \(P=\dfrac{4x-1}{2x+3}\inℤ\left(x\inℤ;x\ne-\dfrac{3}{2}\right)\)
\(\Rightarrow4x-1⋮2x+3\)
\(\Rightarrow4x-1-2\left(2x+3\right)⋮2x+3\)
\(\Rightarrow4x-1-4x-6⋮2x+3\)
\(\Rightarrow-7⋮2x+3\)
\(\Rightarrow2x+3\in\left\{-1;1;-7;7\right\}\)
\(\Rightarrow x\in\left\{-2;-1;-5;2\right\}\)
a) P=\(\dfrac{2x+5}{x+3}=\dfrac{2\left(x+3\right)-2}{x+3}=\dfrac{2\left(x+3\right)}{x+3}-\dfrac{2}{x+3}=2-\dfrac{2}{x+3}\)
để \(P\inℤ\) thì \(\dfrac{2}{x+3}\inℤ\) hay 2 ⋮ (x-3) ⇒x+3 ϵ Ư2= (2,-2,1,-1)
ta có bảng sau:
Vậy x \(\in-1,-2,-5,-4\)