Tìm x ∈ N biet (x...

∈ N biet (x...">

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

NT

NGUYỄN THU HÀ

30 tháng 10 2016

Tìm x N biet (x - 2)(2x - 1) = 35

P/s: nho giai day du chi tiet nha

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 2 2022

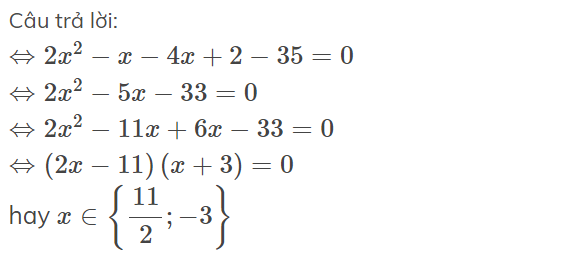
undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NT

NGUYỄN THU HÀ

30 tháng 10 2016

Tìm x bieets:

a) x + 17 ⋮ (x - 12)

b) 3x + 6 ⋮ (x - 3)

P/s: giai day du va chi tiet minh se tick

#Hỏi cộng đồng OLM #Toán lớp 8

1

PA

Phương An

30 tháng 10 2016

undefined

DL

do linh

2 tháng 3 2018 - olm

Tim min cua \(C=\frac{2x+1}{x^2+2}\)

CAC BN GIAI CHI TIET GIUM MK NHA !

#Hỏi cộng đồng OLM #Toán lớp 8

2

PT

Phạm Tuấn Đạt

2 tháng 3 2018

2C = 4x+2/x^2+2

2C + 1 = 4x+2+x^2+2/x^2+2

= x^2+4x+4/x^2+2

= (x+2)^2/x^2+2 > = 0

<=> 2C >= -1

<=> C >= -1/2

Dấu "=" xảy ra <=> x+2=0 <=> x=-2

Vậy Min của C = -1/2 <=> x=-2

NA

Nguyễn Anh Quân

2 tháng 3 2018

2C = 4x+2/x^2+2

2C + 1 = 4x+2+x^2+2/x^2+2

= x^2+4x+4/x^2+2

= (x+2)^2/x^2+2 > = 0

<=> 2C >= -1

<=> C >= -1/2

Dấu "=" xảy ra <=> x+2=0 <=> x=-2

Vậy Min của C = -1/2 <=> x=-2

Tk mk nha

NT

Nguyễn Thắng Thịnh

3 tháng 10 2016

tìm GTLN a) 4- x2x2 + 2x b) 4x - x2x2 c) -4x2x2 + 2x - 5help me !!!! ( Ai nhanh được 5 tick nhé...

#Hỏi cộng đồng OLM #Toán lớp 8

1

DY

Đặng Yến Linh

3 tháng 10 2016

a)= -(x²-2x +1) +1 +4

GTLN = 5

b)= -( x² -4x +4) +4

GTLN = 4

c) = -4( x²- x/4 + 1/16) +1/4 -5

GTLN = -19/5

TT

Trịnh Trọng Khánh

11 tháng 8 2016

giải phương...

#Hỏi cộng đồng OLM #Toán lớp 8

1

NP

Nguyễn Phương HÀ

11 tháng 8 2016

Hỏi đáp Toán

KM

khoi my

31 tháng 8 2018 - olm

Tìm x

-2x\(^2\)+ 5x = 16

giai chi tiết giúp mình nha

#Hỏi cộng đồng OLM #Toán lớp 8

1

LN

Lê Ng Hải Anh

31 tháng 8 2018

\(-2x^2+5x=16\)

\(-2x^2+5x-16=0\)

\(-\left(2x^2-5x+16\right)=0\)

\(2x^2-5x+16=0\)

\(2\left(x^2-\frac{5}{2}x+8\right)=0\)

\(x^2-\frac{5}{2}x+8=0\)

\(x^2-\frac{5}{2}x+\frac{25}{16}+\frac{103}{16}=0\)

\(\left(x-\frac{5}{4}\right)^2+\frac{103}{16}=0\)

Ta có: \(\left(x-\frac{5}{4}\right)^2\ge0\forall x\)

\(\Rightarrow\left(x-\frac{5}{4}\right)^2+\frac{103}{16}\ge\frac{103}{16}>0\)

Mà: \(\left(x-\frac{5}{4}\right)^2+\frac{103}{16}=0\)

=> Vô lí

Vậy : ko có giá trị thỏa mãn của x

=.= hok tốt!!

NT

Nguyễn Thị Hồng Ngọc

15 tháng 12 2016

1: Làm tính nhâna, 2x.(x2 -7x-3)b, (−2x3+34y2−7xy).4xy2(−2x3+34y2−7xy).4xy2c, ( x2 -2x+3).(x-4)d , ( 2x3 - 3x-1).(5x+2)2 phân tích các đa thức sau thành nhân tử :a, x3 -2x2+xb , x2−2x−15x2−2x−15c , y(x-z)+7(z-x)d, 36 - 12x +...

#Hỏi cộng đồng OLM #Toán lớp 8

2

LF

Lightning Farron

15 tháng 12 2016

Bài 2:

a)\(x^3-2x^2+x\)

\(=x\left(x^2-2x+1\right)\)

\(=x\left(x-1\right)^2\)

b)\(x^2-2x-15\)

\(=x^2-5x+3x-15\)

\(=x\left(x-5\right)+3\left(x-5\right)\)

c)\(y\left(x-z\right)+7\left(z-x\right)\)

\(=7\left(z-x\right)-y\left(z-x\right)\)

\(=\left(7-y\right)\left(z-x\right)\)

\(=\left(x-5\right)\left(x+3\right)\)

d)\(36-12x+x^2\)

\(=x^2-12x+36\)

\(=\left(x-6\right)^2\)

LF

Lightning Farron

15 tháng 12 2016

Bài 1:

a)\(2x\left(x^2-7x-3\right)=2x^3-14x^2-6x\)

b)\(\left(-2x^3+34y^2-7xy\right)\cdot4xy^2=136xy^4-28x^2y^3-8x^4y^2\)

c)\(\left(x^2-2x+3\right)\left(x-4\right)\)

\(=x^2\left(x-4\right)-2x\left(x-4\right)+3\left(x-4\right)\)

\(=x^3-4x^2-2x^2+8x+3x-12\)

\(=x^3-6x^2+11x-12\)

d)\(\left(2x^3-3x-1\right)\left(5x+2\right)\)

\(=5x\left(2x^3-3x-1\right)+2\left(2x^3-3x-1\right)\)

\(=10x^4-15x^2-5x+4x^3-6x-2\)

\(=10x^4+4x^3-15x^2-11x-2\)

HL

Han Luu Ngoc

30 tháng 7 2015 - olm

Rut gon

a)\(\left(x-4\right)\left(x+4\right)x-\left(x^2+1\right)\left(x^2-1\right)\)

b)\(\left(y-3\right)\left(y+3\right)\left(y^2+9\right)-\left(y^2+2\right)\left(y^2-2\right)\)

c)\(x\left(x+\frac{1}{2}\right)-\left(2x-1\right)\left(x+\frac{3}{4}\right)\)

giai chi tiet giup minh nhe

#Hỏi cộng đồng OLM #Toán lớp 8

1

ND

nguyễn Đăng khôi

30 tháng 7 2015

a/-x⁴+x³-16x+1

b/-77

c/\(\frac{-4x^2+3}{4}\)

NN

Nguyễn Ngọc Phượng

21 tháng 8 2016

Tìm GTNN hoặc GTLN của các biểu thức...

#Hỏi cộng đồng OLM #Toán lớp 8

2

IM

Isolde Moria

21 tháng 8 2016

a)

Ta có

\(\left(2x-3\right)^2\ge0\) với mọi x

Dấu " = " xảy ra khi \(2x-3=0\Leftrightarrow x=\frac{3}{2}\)

Vậy MIN_A=0 khi x=3/2

b)

Ta có

\(\left|2-3x\right|\ge0\) với mọi x

\(\Rightarrow-\left|2-3x\right|\le0\)

\(\Rightarrow\frac{1}{2}-\left|2-3x\right|\le\frac{1}{2}\)

Dấu " = " xảy ra khi x=2/3

Vậy MAX_B=1/2 khi x=2/3

VD

Võ Đông Anh Tuấn

21 tháng 8 2016

a ) đề sai

b ) \(B=\frac{1}{2}-\left|2-3x\right|\)

Vì :\(\left|2-3x\right|\ge0\)

\(\Rightarrow-\left|2-3x\right|\le0\)

\(\Rightarrow\frac{1}{2}-\left|2-3x\right|\le\frac{1}{2}\)

Vậy GTNN của \(B=\frac{1}{2}\)

MM

Mei Mei

25 tháng 7 2018

quy đồng mẫu thức các phân thức sau:

a. \(\dfrac{1}{x+2}\), \(\dfrac{8}{2x-x^2}\)

b. \(x^2+1,\dfrac{x^4}{x^2-1}\)

làm chi tiết nha mn tks

#Hỏi cộng đồng OLM #Toán lớp 8

1

LT

lê thị hương giang

20 tháng 8 2018

a, \(2x-x^2=x\left(2-x\right)\)

\(MC=x\left(2-x\right)\left(x+2\right)\)

\(\dfrac{1}{x+2}=\dfrac{x\left(2-x\right)}{x\left(2-x\right)\left(x+2\right)}\);\(\dfrac{8}{2x-x^2}=\dfrac{8\left(x+2\right)}{x\left(2-x\right)\left(x+2\right)}\)

b,

MC : \(x^2-1\)

\(x^2+1=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\) ; \(\dfrac{x^4}{x^2-1}\)

MM

Mei Mei

20 tháng 8 2018

lê thị hương giang bạn giải thích cho mình với, chỗ câu a ấy, sao lại ra đc mẫu chung như vậy? rồi cả câu b nữa