Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x + 17 chia hết cho x - 12
<=> x - 12 + 29 chia hết cho x - 12
<=> 29 chia hết cho x - 12
<=> x - 12 thuộc Ư(29) = {-29 ; -1 ; 1 ; 29}
<=> x thuộc {-17 ; 11 ; 13 ; 41}
3x + 6 chia hết x - 3
<=> 3x - 9 + 15 chia hết x - 3
<=> 3(x - 3) + 15 chia hết x - 3
<=> 15 chia hết x - 3
<=> x - 3 thuộc Ư(15) = {-15 ; -5 ; -3 ; -1 ; 1 ; 3 ; 5 ; 15}
<=> x thuộc {-12 ; -2 ; 0 ; 2 ; 4 ; 6 ; 8 ; 18}
a) x + 17 ⋮ (x - 12)
=>(19 + x - 12) \(⋮\) (x - 12)
=>19 \(⋮\) (x - 12)
=>(x -12)\(\in\) {1;19}
=>x \(\in\) {13;31}
Mk giải đúng ko vậy ?

ta thấy \(2x^2+7>0\)
\(=>-3x-9< 0\)
\(=>-3x< 9\)
\(=>x>-3\)
vậy...

b,\(\Rightarrow\)\(\left(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x\left(x+1\right)}\right):2=\frac{2013}{2015}:2\)
\(\Rightarrow\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{x\left(x+1\right)}=\frac{2013}{4030}\)
\(\Rightarrow\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{x.\left(x+1\right)}=\frac{2013}{4030}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{2013}{4030}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{2013}{4030}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{2015}\)
\(\Rightarrow\)\(x+1=2015\)
\(\Rightarrow x=2014\)
a, 2/3x -3/2.x-1/2x=5/12
x.(2/3-3/2-1/2)=5/12
x. -4/3=5/12
x=5/12:-4/3
x=-5/16
b,2/6+2/12+2/20+...+2/x.(x+1)=2013/2015
2/2.3+2/3.4+2/4.5+...+2/x.(x+1)=2013/2015
1/2(1-1/3+1/3-1/4+1/4-1/5+...+1/x-1/x+1)=2013/2015
1/2(1-1/x+1)=2013/2015
1-1/x+1=2013/2015 : 1/2
1-1/x+1=4206/2015
suy ra đề sai

do \(\frac{1}{n}\)và \(\frac{1}{n+1}\)có cùng tử số
mà 2 phân số có cùng tử số thì phân số có mẫu số lớn hơn thì bé hơn.
lại có : n < n+1
\(\Rightarrow\frac{1}{n}\)> \(\frac{1}{n+1}\)

\(\frac{x+5}{7-x}\)= \(\frac{2}{-5}\)
-5x - 25 = 14 - 2x
- 3x = 39
x = -13
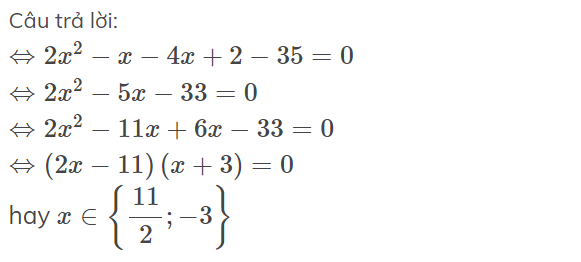
\(\Leftrightarrow2x^2-x-4x+2-35=0\)
\(\Leftrightarrow2x^2-5x-33=0\)
\(\Leftrightarrow2x^2-11x+6x-33=0\)
\(\Leftrightarrow\left(2x-11\right)\left(x+3\right)=0\)
hay \(x\in\left\{\dfrac{11}{2};-3\right\}\)