Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x+1\right)^3+\left(x-2\right)^3-2x^2\left(x-1,5\right)=3\)
\(\Leftrightarrow x^3+3x^2+3x+1+x^3-6x^2+12x-8-2x^3+3x^2=3\)
\(\Leftrightarrow15x=10\Leftrightarrow x=\dfrac{2}{3}\)

c)
\(x^3-3.x^2.6+3.x.6^2-6^3=0\)
\(\left(x-6\right)^3=0\)
x-6=0
x=6
d)
\(x^3-3.x^2.1+3.x.1^2-1-x^3-3x-2=0\)
\(x^3-3x^2+3x-1-x^3-3x^2-2=0\)
\(-6x^2-3=0\)
\(-3\left(2x^2+1\right)=0\)
\(2x^2+1=0\)
2x2=-1
x2=1/2
x=\(\dfrac{\sqrt{2}}{2}\)

Pt $\Leftrightarrow (x-4)^3=0\\\Leftrightarrow x-4=0\\\Leftrightarrow x=4$

a)
\(\left(3x\right)^3-3.\left(3x\right)^2.1+3.3x.2^2-2^3=0\)
\(\left(3x-2\right)^3=0\)
3x-2=0
3x=2
x=2/3
b)
\(x^3-3.x^2.5+3.x.5^2+5^3=0\)
\(\left(x-5\right)^3=0\)
x-5=0
x=5

\(a,\Leftrightarrow\left(x^2-3\right)^2=0\\ \Leftrightarrow x^2-3=0\\ \Leftrightarrow\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\\ b,\Leftrightarrow8x^3+12x^2+6x+1-64=0\\ \Leftrightarrow\left(2x+1\right)^3-4^3=0\\ \Leftrightarrow\left(2x+1-4\right)\left[\left(2x+1\right)^2+4\left(2x+1\right)+16\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=3\\4x^2+4x+1+8x+4+16=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\4x^2+12x+17=0\left(1\right)\end{matrix}\right.\)
Xét \(\left(1\right)\Leftrightarrow\left(2x+3\right)^2+8=0\left(vô.lí\right)\Leftrightarrow x\in\varnothing\)
Vậy pt có nghiệm \(x=\dfrac{3}{2}\)
\(c,\Leftrightarrow\left(3-2x-5\right)\left(3-2x+5\right)=0\\ \Leftrightarrow\left(-2-2x\right)\left(8-2x\right)=0\\ \Leftrightarrow-2\left(x+1\right)\cdot2\left(4-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)

c: Ta có: \(x^3-12x^2+48x-64=0\)
\(\Leftrightarrow x-4=0\)
hay x=4

c: Ta có: \(x^3-12x^2+48x-64=0\)
\(\Leftrightarrow x-4=0\)
hay x=4
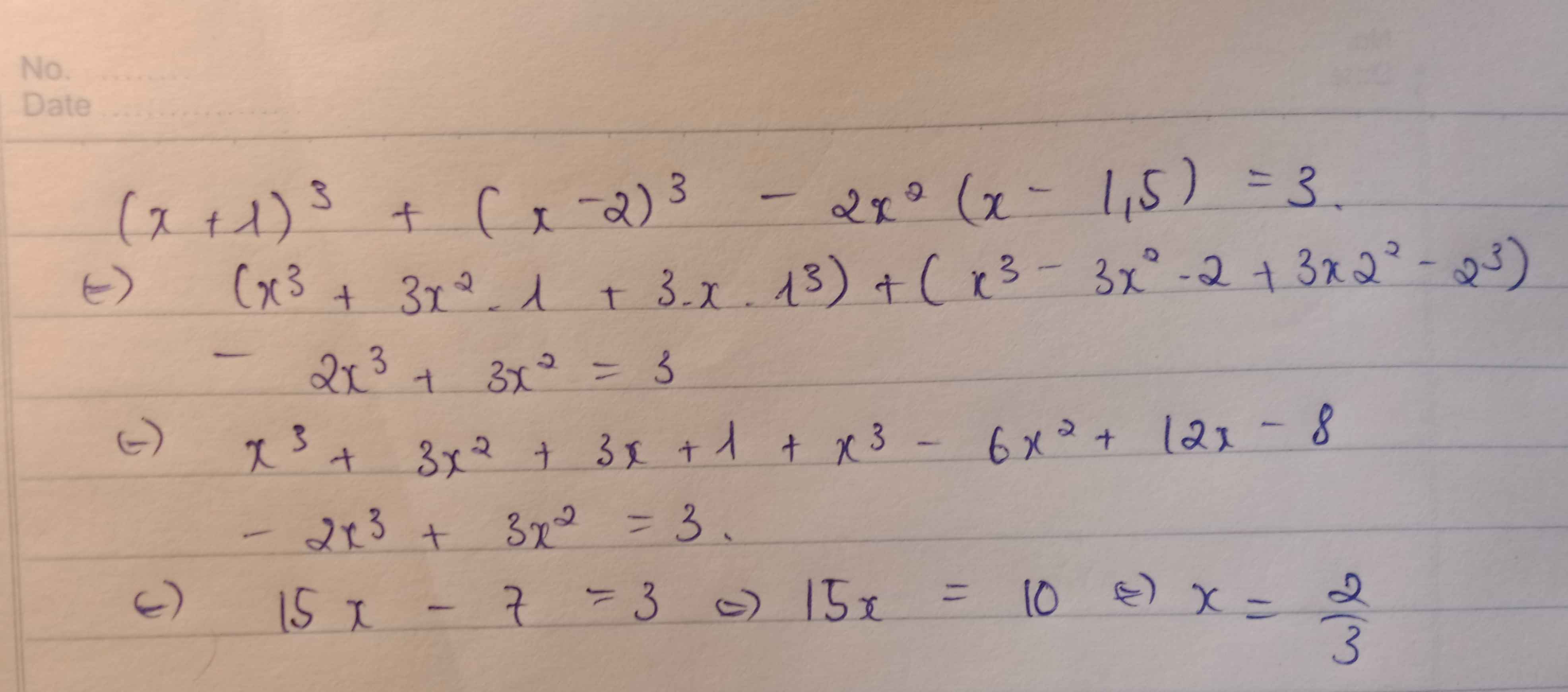
\(36x^2-121=0\)
\(x^2=\dfrac{121}{36}\)
\(x=\dfrac{11}{6}\) hoặc \(x=\dfrac{-11}{6}\)
\(36x^2-121=0\)
\(\Leftrightarrow\)\(36x^2=121\)
\(\Leftrightarrow\)\(x^2=\)\(\dfrac{121}{36}\)
\(\Leftrightarrow\)\(x=\)\(\dfrac{11}{6}\)