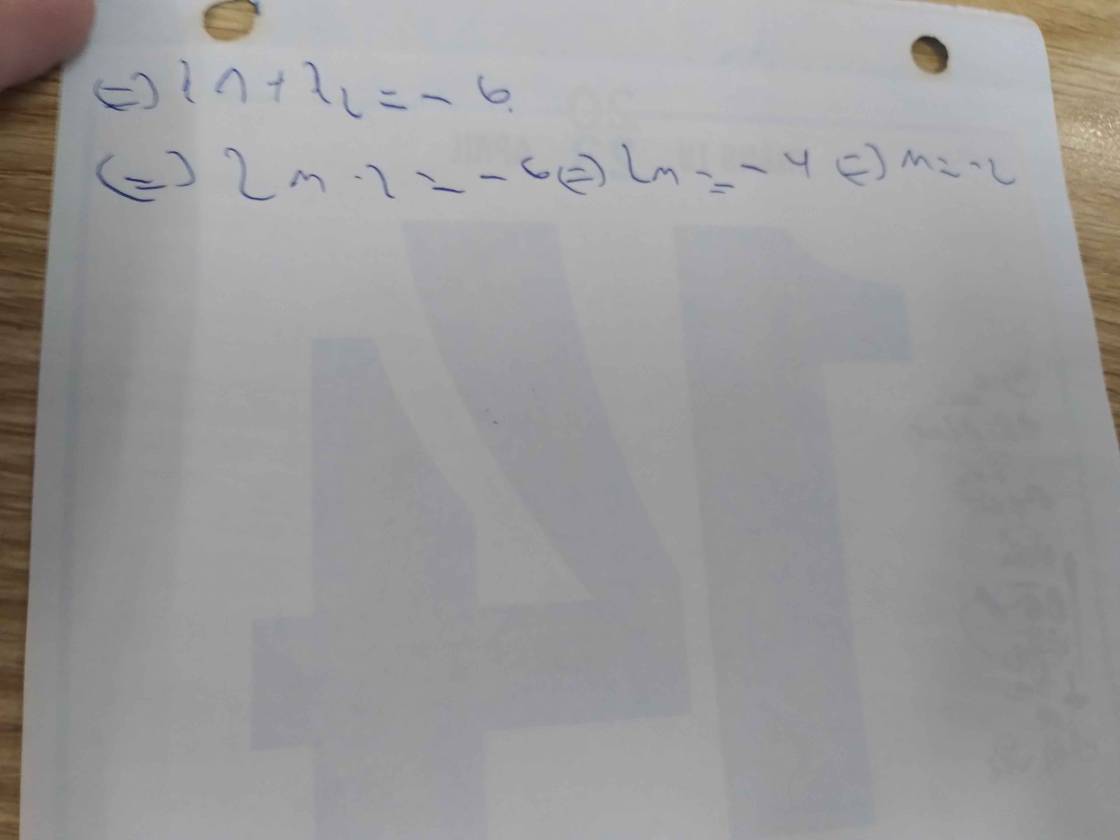Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$(x^2+x)(x^2+11x+30)+7=x(x+1)(x+5)(x+6)+7$
$=(x^2+6x)(x^2+6x+5)+7$
$=(x^2+6x)^2+5(x^2+6x)+7$
$=(x^2+6x+\frac{5}{2})^2+\frac{3}{4}\geq \frac{3}{4}$ với mọi $x\in\mathbb{R}$
Do đó $\frac{3}{4}\geq k$ nên $k_{\max}=\frac{3}{4}$

\(x+y=35\Rightarrow y=35-x\)
Thế vào \(x^2+y^2=625\)
\(\Rightarrow x^2+\left(35-x\right)^2=625\)
\(\Leftrightarrow2x^2-70x+600=0\)
\(\Rightarrow\left[{}\begin{matrix}x=15\Rightarrow y=20\\x=20\Rightarrow y=15\end{matrix}\right.\)

Đặt \(x+2=t\Rightarrow x=t-2\)
\(\Rightarrow f\left(t\right)=\left(t-2\right)^2-3\left(t-2\right)+1=t^2-7t+11\)
\(\Rightarrow f\left(x\right)=x^2-7x+11\)

a) √x2 = 7 ⇔ |x| = 7
⇔ x1 = 7 và x2 = -7
b) √x2 = |-8| ⇔ √x2 = 8
⇔ |x| = 8 ⇔ x1 = 8 và x2 = -8
![]()
⇔ |x| = 3 ⇔ x1 = 3 và x2 = -3
![]()
⇔ |3x| = 12 ⇔ |x| = 4
⇔ x1 = 4 và x2 = -4

Vì (1 - x)2 ≥ 0 ∀x nên phương trình xác định với mọi giá trị của x.
![]()
- Khi 1 – x ≥ 0 ⇔ x ≤ 1
Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6
⇔ –2x = 4 ⇔ x = –2 (nhận)
- Khi 1 – x < 0 ⇔ x > 1
Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6
⇔ x – 1 = 3 ⇔ x = 4 (nhận)
Vậy phương trình có hai nghiệm: x = - 2; x = 4