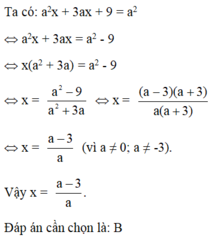Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a^2x+3ax+9=a^2\)
\(a^2x+3ax+9-a^2=0\)
\(ax\left(a+3\right)+\left(3-a\right)\left(a+3\right)=0\)
\(\left(a+3\right)\left(ax+3-a\right)=0\)
\(\left(a+3\right)\left[a\left(x-1\right)+3\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}a+3=0\\a\left(x-1\right)+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}a=-3\left(L\right)\\a=\left\{\pm1;3\right\}\left(N\right);a=-3\left(L\right)\end{cases}}\)
Vậy \(a=\left\{\pm1;3\right\}\)

em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.

Ta có: \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+b^2y^2+2axby\)
\(\Leftrightarrow a^2y^2-2axby+b^2x^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\)
\(\Leftrightarrow ay=bx\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Ta có : \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2abxy+b^2y^2\)
\(\Leftrightarrow a^2y^2-2abxy+b^2x^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\)
\(\Leftrightarrow ay-bx=0\)
\(\Leftrightarrow ay=bx\Leftrightarrow\dfrac{a}{b}=\dfrac{x}{y}\)