K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
2
AH
Akai Haruma
Giáo viên
27 tháng 6 2023
1.
$(3^2-2^3)x+3^2.2^2=4^2.3$
$\Leftrightarrow x+36=48$
$\Leftrightarrow x=48-36=12$
2.
$x^5-x^3=0$
$\Leftrightarrow x^3(x^2-1)=0$
$\Leftrightarrow x^3(x-1)(x+1)=0$
$\Leftrightarrow x^3=0$ hoặc $x-1=0$ hoặc $x+1=0$
$\Leftrightarrow x=0$ hoặc $x=\pm 1$
3.
$(x-1)^2+(-3)^2=5^2(-1)^{100}$
$\Leftrightarrow (x-1)^2+9=25$
$\Leftrightarrow (x-1)^2=25-9=16=4^2=(-4)^2$
$\Rightarrow x-1=4$ hoặc $x-1=-4$
$\Leftrightarrow x=5$ hoặc $x=-3$
4.
$(2x-1)^2-(2x-1)=0$
$\Leftrightarrow (2x-1)(2x-1-1)=0$
$\Leftrightarrow (2x-1)(2x-2)=0$
$\Leftrightarrow 2x-1=0$ hoặc $2x-2=0$
$\Leftrightarrow x=\frac{1}{2}$ hoặc $x=1$
$\Lef
27 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
\((3^2-2^3)x+3^2.2^2=4^2.3\)
`=> x + (3*2)^2 = 48`
`=> x+6^2 = 48`
`=> x + 36 = 48`
`=> x = 48 - 36`
`=> x=12`
Vậy, `x=12`
\(x^5-x^3=0\)
`=> x^3(x^2 - 1)=0`
`=>`\(\left[{}\begin{matrix}x^3=0\\x^2-1=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=0\\x^2=1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=0\\x=\pm1\end{matrix}\right.\)
Vậy, `x \in {0; +- 1 }`
\(\left(x-1\right)^2+\left(-3\right)^2=5^2\cdot\left(-1\right)^{100}\)
`=> (x-1)^2 + 9 = 25*1`
`=> (x-1)^2 + 9 = 25`
`=> (x-1)^2 = 25 - 9`
`=> (x-1)^2 = 16`
`=> (x-1)^2 = (+-4)^2`
`=>`\(\left[{}\begin{matrix}x-1=4\\x-1=-4\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4+1\\x=-4+1\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)
Vậy, `x \in {5; -3}`
\((2x-1)^2-(2x-1)=0\)
`=> (2x-1)(2x-1) - (2x-1)=0`
`=> (2x-1)(2x-1-1)=0`
`=>`\(\left[{}\begin{matrix}2x-1=0\\2x-2=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}2x=1\\2x=2\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy, `x \in {1; 1/2}`
NM
3
5 tháng 9 2023
`#040911`
`a)`
`2x^2 - 3x = 0`
`\Rightarrow x(2x - 3) = 0`
`\Rightarrow`\(\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\)
`\Rightarrow`\(\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy, \(x\in\left\{0;\dfrac{3}{2}\right\}\)
`b)`
\(x+\dfrac{1}{2}-z-\dfrac{2}{3}=\dfrac{1}{2}?\)
Bạn xem lại đề
`c)`
\(x^3-x^2=0\\ \Rightarrow x^2\cdot\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy, \(x\in\left\{0;1\right\}.\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
5 tháng 9 2023
\(a,2x^2-3x=0\\ \Leftrightarrow x\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\\ b,Xem.lại,đề\\ c,x^3-x^2=0\\ \Leftrightarrow x^2.\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
NH
11 tháng 9 2019
B1: Đk: 5x ≥ 0 => x ≥ 0
Vì |x + 1| ≥ 0 => |x + 1| = x + 1
|x + 2| ≥ 0 => |x + 2| = x + 2
|x + 3| ≥ 0 => |x + 3| = x + 3
|x + 4| ≥ 0 => |x + 4| = x + 4
=> |x + 1| + |x + 2| + |x + 3| + |x + 4| = 5x
=> x + 1 + x + 2 + x + 3 + x + 4 = 5x
=> 4x + 10 = 5x
=> x = 10
B2: Ta có: |x - 2018| = |2018 - x|
=> A=|x + 2000| + |2018 - x| ≥ |x + 2000 + 2018 - x| = |4018| = 4018
Dấu " = " xảy ra <=> (x + 2000)(x - 2018) ≥ 0
Th1: \(\hept{\begin{cases}x+2000\ge0\\x-2018\ge0\end{cases}\Rightarrow}\hept{\begin{cases}x\ge-2018\\x\le2018\end{cases}}\Rightarrow-2018\le x\le2018\)
Th2: \(\hept{\begin{cases}x+2000\le0\\x-2018\le0\end{cases}\Rightarrow}\hept{\begin{cases}x\le-2018\\x\ge2018\end{cases}}\)(vô lý)
Vậy GTNN của A = 4018 khi -2018 ≤ x ≤ 2018
B3:
a, Vì |x + 1| ≥ 0 ; |2y - 4| ≥ 0
=> |x + 1| + |2y - 4| ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x+1=0\\2y-4=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=2\end{cases}}\)
Vậy...
b, Vì |x - y + 1| ≥ 0 ; (y - 3)2 ≥ 0
=> |x - y + 1| + (y - 3)2 ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x-y+1=0\\y-3=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x-y=-1\\y=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x-3=-1\\y=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=3\end{cases}}\)
Vậy...
c, Vì |x + y| ≥ 0 ; |x - z| ≥ 0 ; |2x - 1| ≥ 0
=> |x + y| + |x - z| + |2x - 1| ≥ 0
Dấu " = " xảy ra <=> \(\hept{\begin{cases}x+y=0\\x-z=0\\2x-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=0\\x=z\\x=\frac{1}{2}\end{cases}\Leftrightarrow}}\hept{\begin{cases}\frac{1}{2}+y=0\\x=z=\frac{1}{2}\end{cases}\Leftrightarrow}\hept{\begin{cases}y=\frac{-1}{2}\\x=z=\frac{1}{2}\end{cases}}\)
HT
1 tháng 9 2015
1, (3x + 1/5).(x - 1/2) = 0
<=> (3x + 1/5) = 0 hoặc (x - 1/2) = 0
<=> 3x = -1/5 hoặc x = 1/2
<=> x = -1/15 hoặc x = 1/2
OP
1
OM
17 tháng 8 2016
A) \(\left(x+1\right).\left(x-2\right)< 0\)
\(=x.\left(x-2\right)+1.\left(x-2\right)< 0\)
\(=x.\left(x-2\right)+\left(x-2\right)< 0\)
\(\Rightarrow x\in Z\)
Vậy \(x>2\)
B)\(\left(x-2\right).\left(x+\frac{2}{3}\right)>0\)
\(x.\left(x+\frac{2}{3}\right)-2\left(x\frac{2}{3}\right)\)
\(\Rightarrow x+\frac{2}{3}=sốnguyên\)
Nên \(x\)thuốc phân số.
Câu c) tự làm nha.
12 tháng 7 2019
\(a,\frac{1}{3}+\frac{1}{2}:x=\frac{1}{5}\)
\(\Leftrightarrow\frac{1}{2}:x=\frac{1}{5}-\frac{1}{3}\)
\(\Leftrightarrow\frac{1}{2}:x=\frac{3}{15}-\frac{5}{15}\)
\(\Leftrightarrow\frac{1}{2}:x=\frac{-2}{15}\)
\(\Leftrightarrow x=\frac{1}{2}:\frac{-15}{2}=\frac{-15}{4}\)
12 tháng 7 2019
\(b,\frac{1}{3}x+\frac{2}{5}\left[x+1\right]=0\)
\(\Leftrightarrow\frac{1}{3}x+\frac{2}{5}x+\frac{2}{5}=0\)
\(\Leftrightarrow\frac{11}{15}x=-\frac{2}{5}\Leftrightarrow x=\frac{-2}{5}:\frac{11}{15}=\frac{-2}{5}\cdot\frac{15}{11}=\frac{-2}{1}\cdot\frac{3}{11}=\frac{-6}{11}\)
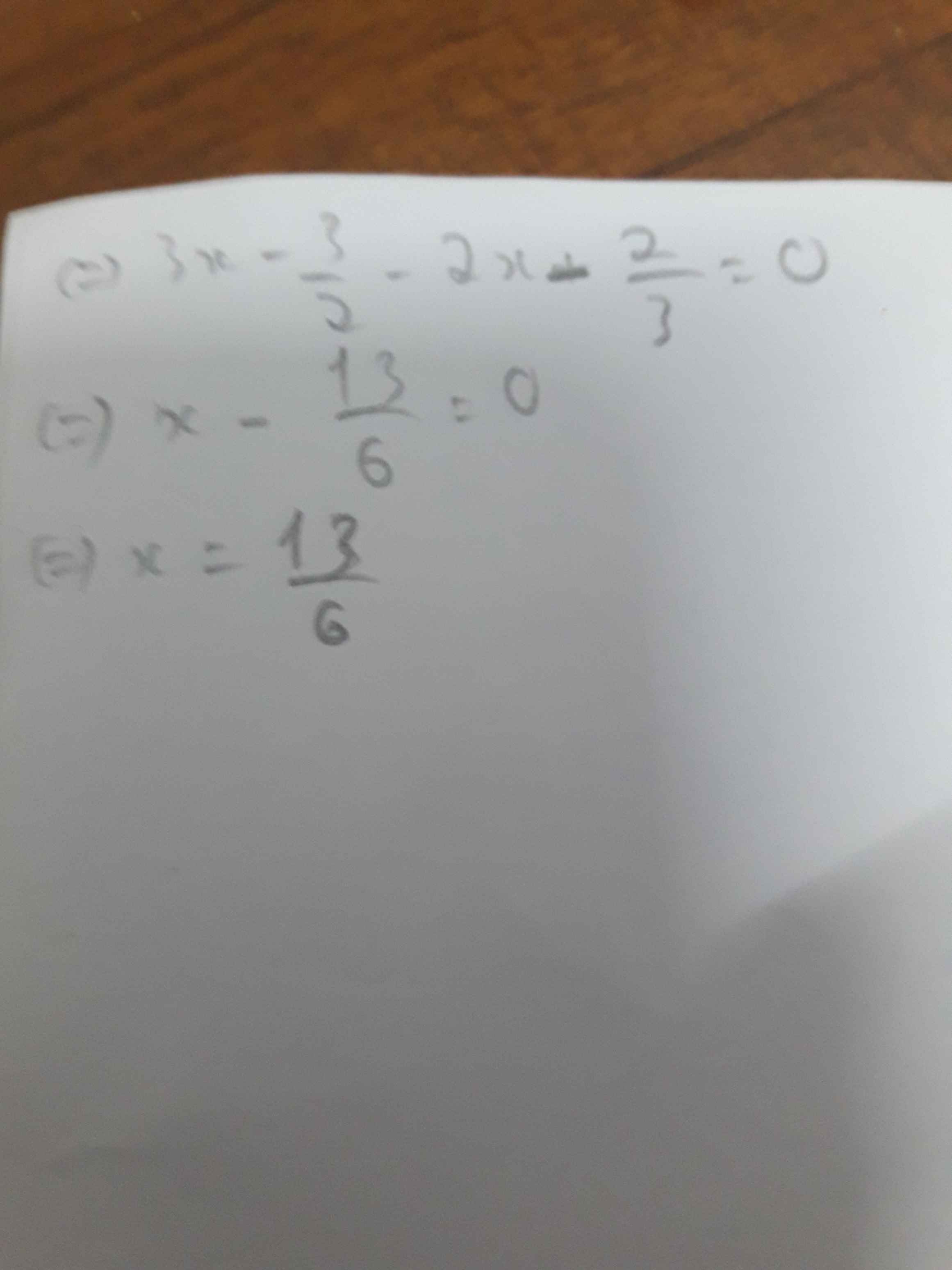
2 x − 1 2 . 3 x − 1 3 < 0
TH1: 2 x − 1 2 > 0 3 x − 1 3 < 0 ⇔ 2 x > 1 2 3 x < 1 3 ⇔ x > 1 4 x < 1 9 ⇒ không tìm được x
TH2: 2 x − 1 2 < 0 3 x − 1 3 > 0 ⇔ 2 x < 1 2 3 x > 1 3 ⇔ x < 1 4 x > 1 9 ⇔ 1 9 < x < 1 4
Vậy: 1 9 < x < 1 4