
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



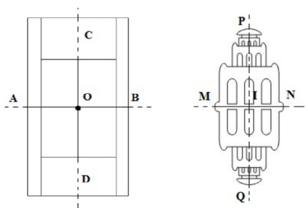
a) Hình 110 (sân quần vợt) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng AB và CD.
-Một tâm đối xứng là O.
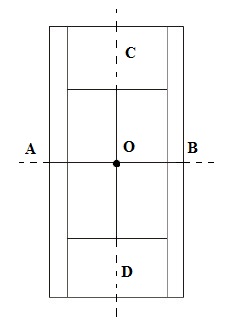
b) Hình 111 (Tháp Rùa và bóng của nó trên mặt nước) có hai trục đối xứng, có một tâm đối xứng.
-Hai trục đối xứng là MN và PQ.
- Một tâm đối xứng là I.
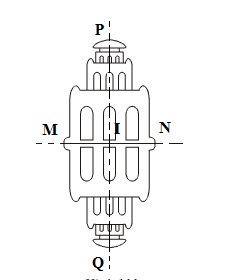
a) Hình 45 (sân quần vợt) có hai trục đối xứng, có một tâm đối xứng.
- Hai trục đối xứng AB và CD.
- Một tâm đối xứng là O.
b) Hình 46 (Tháp Rùa và bóng của nó trên mặt nước) có hai trục đối xứng, có một tâm đối xứng.
- Hai trục đối xứng là MN và PQ
- Một tâm đối xứng là I.

Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn

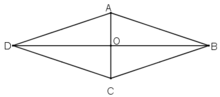
a) ABCD là hình thoi
⇒ ABCD là hình bình hành
⇒ giao điểm O của AC và BD là tâm đối xứng của ABCD.
b)
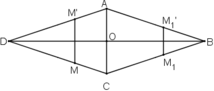
ét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có:
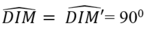
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
=> ∆ DIM = ∆ DIM’ ( c.g.c)
=> DM = DM’ và 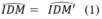
Lại có: ABCD là hình thoi nên
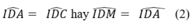
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.

Những hình có trục đối xứng là: đường tròn, tam giác cân, tam giác đều, hình thang cân, hình thoi, hình vuông, hình chữ nhật
Những hình có tâm đối xứng là: đường tròn, hình bình hành, hình chữ nhật, hình thoi, hình vuông
Những hình vừa có tâm đối xứng vừa có trục đối xứng là: hình chữ nhật, hình thoi, hình vuông