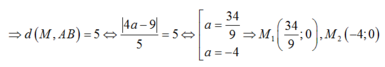Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a: y=ax+b
a=tan alpha=1
=>y=x+b
Thay x=-1 và y=1 vào (d), ta được:
b-1=1
=>b=2
=>y=x+2
d: (Δ)//(d) nên Δ: 3x+4y+c=0
(C): x^2+y^2-2x+2y-7=0
=>x^2-2x+1+y^2+2y+1=9
=>(x-1)^2+(y+1)^2=9
=>R=3; I(1;-1)
Theo đề, ta có: d(I;Δ)=3
=>\(\dfrac{\left|1\cdot3+\left(-1\right)\cdot4+c\right|}{\sqrt{3^2+4^2}}=3\)
=>|c-1|=3*5=15
=>c=16 hoặc c=-14

Lời giải:
a. Gọi ptđt $AB$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -1=2a+b\\ 3=-5a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-4}{7}\\ b=\frac{1}{7}\end{matrix}\right.\)
Vậy ptđt $AB$ là $y=\frac{-4}{7}x+\frac{1}{7}$
$M\in Ox$ nên $y_M=0$
$M\in AB$ nên: $y_M=\frac{-4}{7}x_M+\frac{1}{7}$
$\Leftrightarrow 0=\frac{-4}{7}x_M+\frac{1}{7}$
$\Rightarrow x_M=\frac{1}{4}$
Vậy $M(\frac{1}{4}, 0)$
b. Gọi giao điểm của $Oy$ và $AB$ là $(0,a)$.
Do điểm này thuộc $AB$ nên:
$a=\frac{-4}{7}.0+\frac{1}{7}=\frac{1}{7}$
Vậy $(0,\frac{1}{7})$ là giao của $AB$ và trục $Oy$

Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5