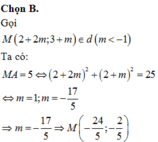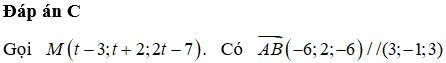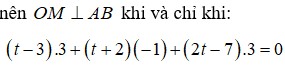Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Gọi H(1 +2t; -3 +t; -2t) là hình chiếu
vuông góc của M trên d
Khi đó
M H ¯ = − 1 + 2 t ; 3 + t ; − 4 − 2 t .
Cho
M H ¯ . u d ¯ = − 2 + 4 t + 3 + t + 8 + 4 t = 0 ⇔ t = − 1
Suy ra H − 1 ; − 4 ; 2 ⇒ M ' − 4 ; − 2 ; 0 .
Đáp án C
d : x = − 1 + 2 t y = − 2 − t , t ∈ ℝ z = 2 t .
Gọi H là hình chiếu của M trên d ⇒ H − 1 + 2 t ; − 2 − t ; 2 t .
⇒ M H → = − 3 + 2 t ; 1 − t ; − 1 + 2 t
Ta có − 3 + 2 t .2 + 1 − t . − 1 + − 1 + 2 t .2 = 0 ⇔ t = 1 ⇒ H 1 ; − 3 ; 2
Suy ra M ' 0 ; − 3 ; 3 .
Đáp án A
Phương pháp giải:
Vì điểm M thuộc d nên tham số hóa tọa độ điểm M, tính tổng M A 2 + M B 2 đưa về khảo sát hàm số để tìm giá trị nhỏ nhất
Lời giải:
Vì 
suy ra
A
M
→
=
(
t
-
2
;
4
-
2
t
;
2
t
)
B
M
→
=
(
t
;
2
-
2
t
;
2
t
-
2
)
Khi đó 
Dễ thấy 
Vậy Tmin = 10. Dấu bằng xảy ra khi và chỉ khi t = 1 => M(2;0;5)