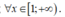Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y'= \(4x^3-4\left(m-1\right)x\)
Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)
\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)
\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)
Vậy \(m\in\) (−\(\infty\);2]

Câu 1:
\(y'=f\left(x\right)=mx^2+14mx+14\)
- Với \(m=0\Rightarrow y'=14>0\Rightarrow y\) đồng biến trên R (ko thỏa mãn)
- Với \(m\ne0\) để hàm số nghịch biến trên \(\left[1;+\infty\right]\) ta có các trường hợp sau:
TH1: \(\left\{{}\begin{matrix}m< 0\\\Delta'=49m^2-14m\le0\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
TH2: \(\left\{{}\begin{matrix}m< 0\\\Delta'>0\\x_1< x_2\le1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m.f\left(1\right)\ge0\\\frac{x_1+x_2}{2}< 1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m\left(15m+14\right)\ge0\\-7< 1\end{matrix}\right.\) \(\Rightarrow m\le-\frac{14}{15}\)
Câu 2:
\(y'=1-msinx\)
Để hàm số đồng biến trên R \(\Leftrightarrow1-m.sinx\ge0\) \(\forall x\)
\(\Leftrightarrow msinx\le1\)
- Với \(m=0\Rightarrow0< 1\) (đúng)
- Với \(m< 0\Rightarrow sinx\ge\frac{1}{m}\Rightarrow\frac{1}{m}\le\min\limits_{x\in R}\left(sinx\right)=-1\)
\(\Rightarrow\frac{m+1}{m}\le0\Rightarrow-1\le m< 0\)
- Với \(m>0\Rightarrow sinx\le\frac{1}{m}\Rightarrow\frac{1}{m}\ge\max\limits_{x\in R}\left(sinx\right)=1\)
\(\Rightarrow\frac{1-m}{m}\ge0\Rightarrow0< m\le1\)
Kết hợp lại ta được \(-1\le m\le1\)

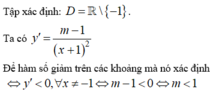
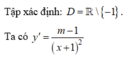

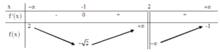

Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
Tương đương với
Dễ dàng có được g(x) là hàm tăng