Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

Ta có : \(y'=3x^2-6mx+3\left(m^2-1\right)\)
Để hàm số có cực trị thì phương trình \(y'=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow x^2-2mx+m^2-1=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1>0\) với mọi m
Cực đại của đồ thị hàm số là A(m-1;2-2m) và cực tiểu của đồ thị hàm số là B (m+1; -2-2m)
Theo giả thiết ta có :
\(OA=\sqrt{2}OB\Leftrightarrow m^2+6m+1\Leftrightarrow\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
Vậy có 2 giá trị m là \(\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
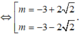

Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
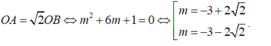
Tổng hai giá trị này là -6.
Chọn C.

Ta có \(y'=3x^2-3\left(m-2\right)x-3\left(m-1\right)\), với mọi \(x\in R\)
\(y'=0\Leftrightarrow x^2-\left(m-2\right)x-m+1=0\Leftrightarrow x_1=-1;x_2=m-1\)
Chú ý rằng với m > 0 thì \(x_1< x_2\). Khi đó hàm số đạt cực đại tại \(x_1=-1\) và đạt cực tiểu tại \(x_2=m-1\). Do đó :
\(y_{CD}=y\left(-1\right)=\frac{3m}{2};y_{CT}=y\left(m-1\right)=-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\)
Từ giả thiết ta có \(2.\frac{3m}{2}-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\Leftrightarrow6m-6-\left(m+2\right)\left(m-1\right)^2=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m-8\right)=0\Leftrightarrow m=1;m=\frac{-1\pm\sqrt{33}}{2}\)
Đối chiếu yêu cầu m > 0, ta có giá trị cần tìm là \(m=1;m=\frac{-1\pm\sqrt{33}}{2}\)

\(\Leftrightarrow y'=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1\)<\(x_2\)<1
\(\Leftrightarrow\)\(\begin{cases}\Delta'=4m^2-m-5>0\\f\left(1\right)=-5m+7>0\\\frac{S}{2}=\frac{2m-1}{3}<1\end{cases}\)\(\Leftrightarrow\)\(\frac{5}{4}\)<m<\(\frac{7}{5}\)

Với mọi \(x\in R,y'=3x^2+6mx\Rightarrow y'=0\Leftrightarrow x=0\) hoặc \(x=-2m\)
Để hàm số có cực đại, cực tiểu thì phương trình \(y'=0\) có 2 nghiệm phân biệt \(\Leftrightarrow m\ne0\). Khi đó, tọa độ các điểm cực trị là \(A\left(0;2\right),B\left(-2m;4m^3+2\right)\)
\(S_{OAB}=1\Leftrightarrow OA.d\left(B;OA\right)=4\Leftrightarrow\left|2\right|=2\Leftrightarrow\begin{cases}m=1\\m=-1\end{cases}\) (thỏa mãn)
Vậy với \(m=\pm1\) thì hàm số có 2 cực trị thỏa mãn bài

Ta có \(y=4x^3-4mx=4x\left(x^2-m\right)=0\Leftrightarrow x=0\) hoặc \(x^2=m\)
Hàm số đã cho có 3 điểm cực trị \(\Leftrightarrow\) phương trình y' = 0 có 3 nghiệm phân biệt và y' đổi dấu khi x đi qua các nghiệm đó <=> m > 0. Khi đó 3 điểm cực trị của đồ thị hàm số là :
\(A\left(0;m-1\right);B\left(-\sqrt{m};m^2+m-1\right);C\left(\sqrt{m};-m^2+m-1\right)\)
a) Ta có \(S_{\Delta ABC}=\frac{1}{2}\left|y_B-y_A\right|.\left|y_C-y_B\right|=m^2\sqrt{m}\)
\(AB=AC=\sqrt{m^4+m};BC=2\sqrt{m}\)
\(R=\frac{AB.AC.BC}{4S_{\Delta ABC}}=1\Leftrightarrow\frac{\left(m^4+m\right)2\sqrt{m}}{4m^2\sqrt{m}}=1\)
\(\Leftrightarrow m^3-2m+1=0\Leftrightarrow m=1\) hoặc \(m=\frac{\sqrt{5}-1}{2}\)
Vậy \(m=1;m=\frac{\sqrt{5}-1}{2}\) là giá trị cần tìm
b) Vì B, C đối xứng nhau qua trục tung nên BC luôn vuông góc OA
Do đó O là trực tâm tam giác ABC khi và chỉ khi \(\overrightarrow{OB}.\overrightarrow{AC}=0\)
\(\overrightarrow{OB}\left(-\sqrt{m};-m^2+m-1\right);\overrightarrow{AC}\left(\sqrt{m};-m^2\right)\)
Suy ra \(-m-m^2\left(-m^2+m-1\right)=0\Leftrightarrow m\left(-m^3+m^2-m+1\right)=0\)
\(\Leftrightarrow m\left(m-1\right)\left(m^2+1\right)=0\Leftrightarrow m=0\) hoặc m = 1
Vậy m = 0 hoặc m = 1 là giá trị cần tìm
c) Rõ ràng tam giác ABC cân tại A và truyên tuyến kẻ từ A thuộc Oy. Do đó O là trọng tâm của tam giác ABC
<=> \(y_A+2y_B=0\)
\(\Leftrightarrow m-1+2\left(-m^2+m-1\right)=0\)
\(\Leftrightarrow2m^2-3m+3=0\) vô nghiệm
Vậy không tồn tai giá trị m thỏa mãn yêu cầu bài toán
bn ơi cho mk hỏi cái công thức tính S tam giác ABC=1/2|yB-yA|.|yC-yB| ở đâu vậy ạ
Chọn A
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
Để A và B cách đều gốc tọa độ khi và chỉ khi :
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.