Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
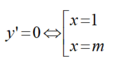
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 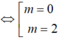
Chọn C.

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

\(y'=4x\left(x-m\right)\left(x+m\right)\\ y'=0\Leftrightarrow\begin{cases}x=0\\x=\pm m\end{cases}\)
Với m=0 thì hàm số có 3 cực trị là 0, -m và m
đồ thị hàm số có 3 điểm cực trị \(A\left(0;1\right),M\left(-m;1-m^4\right),N\left(m;1-m^4\right)\)
Nhận thấy \(AM=AN\) nên \(\Delta AMN\) cân tại A với mọi m
Gọi trung điểm MN là \(I\left(0;1-m^4\right)\)
\(\Delta AMN\) vuông cân tại A khi và chỉ khi \(IA=IM=IN\) hay\(IA=IN\)
\(\Leftrightarrow IA=IN\Leftrightarrow\left|m^4\right|=\left|m\right|\Leftrightarrow m=\pm1\) (vì \(m\ne0\))

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

Chứng minh công thức tổng quát phương trình đi qua 2 điểm cực trị:
giả sử hàm bậc 3: \(y=ax^3+bxx^2+cx+d\left(a\ne0\right)\) có 2 điểm cực trị x1;x2
Ta đi tìm số dư 1 cách tổng quát:
Ta có: \(y'=3ax^2+2bx+c-và-y''=6ax+b\)
Xét phép chia giữa y' và y'' ta có: \(y=y'\left(\dfrac{1}{3}x+\dfrac{b}{9a}\right)+g\left(x\right)\left(1\right)\) là phường trình đi qua 2 điểm cực trị của đồ thị hàm số bậc 3
từ (1) Ta có: \(y=y'\dfrac{3ax+b}{9a}+g\left(x\right)-hay-y=y'\dfrac{6ax+2b}{18a}g\left(x\right)\)
Từ đây dễ suy ra: \(g\left(x\right)=y-\dfrac{y'.y''}{18a}\left(công-thức-tổng-quát\right)\) ( dĩ nhiên bạn chỉ cần nhớ cái này )
áp dụng vào bài toán ta có:
\(2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x-\left(6x^2+6\left(m-1\right)x+6m\left(1-2m\right)\right).\dfrac{12x+6\left(m-1\right)}{18.2}\)
Gán: \(\left\{{}\begin{matrix}x=i\\m=10\end{matrix}\right.\) => 1710-841i
\(\Rightarrow y=4m\left(-2m-1\right)x+17m^2+m\) bài toán quay trở về bài toán đơn giản bạn giải nốt là oke
Khiếp học ghê như vầy bảo dạy người ta thì kêu thôi, sợ sót kiến thức :)))?

+ Đường thẳng đi qua 2 điểm cực trị của hàm số là 2x+ y=0 có VTPT n 1 → ( 2 ; 1 )
+ Đường thẳng đã cho x+ my+ 3= 0 có VTPT n 2 → ( 1 ; m )
Yêu cầu bài toán

Chọn A

Chọn A
Đường thẳng đi qua ĐCĐ, ĐCT là ∆ 1 : 2 x + y = 0 c ó V T P T n 1 ( 2 ; 1 )
Đường thẳng đã cho có ∆ : x + m y + 3 = 0 c ó V T P T n 2 ( 1 ; m )
Yêu cầu bài toán
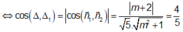
![]()
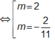

1/ \(y=x^3+3x^2+mx+m-2\)
\(y'=3x^2+6x+m\)
Chia đa thức \(y\) cho \(y'\) được phần dư là \(\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
\(\Rightarrow\)Phương trình đường thẳng \(d\) đi qua 2 cực trị có dạng:
\(y=\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
Gọi A là giao điểm của \(d\) với \(Ox\Rightarrow A\left(-1;0\right)\)
Đồ thị hàm số có 2 cực trị B, C nằm về 2 phía trục hoành khi và chỉ khi A nằm giữa B và C
\(\Rightarrow x_B< -1< x_C\) với \(x_B;x_C\) là nghiệm của pt \(f\left(x\right)=3x^2+6x+m=0\)
\(\Rightarrow3.f\left(-1\right)< 0\Leftrightarrow3\left(3-6+m\right)< 0\Rightarrow m< 3\)
Vậy với \(m< 3\) thì đồ thị hs có 2 cực trị nằm về 2 phía trục hoành
2/
\(y=x^3+3mx^2+m+1\Rightarrow y'=3x^2+6mx\)
Để hàm số có 2 cực trị \(\Rightarrow m\ne0\)
Chia đa thức \(y\) cho \(y'\) được phân dư \(-2m^2x+m+1\)
\(\Rightarrow\) phương trình đường thẳng \(d\) qua 2 cực trị có dạng:
\(y=-2m^2x+m+1\)
Để \(d\) song song đường thẳng \(y=-x+2017\)
\(\Rightarrow\left\{{}\begin{matrix}-2m^2=-1\\m+1\ne2017\end{matrix}\right.\) \(\Rightarrow m=\pm\dfrac{\sqrt{2}}{2}\)
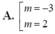

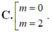
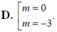
Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2