Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+....+\frac{1}{n\left(n+1\right)}=A\)
\(\Leftrightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{n}-\frac{1}{n+1}\)
\(\Leftrightarrow A=\frac{n+1}{n+1}-\frac{1}{n+1}=\frac{n}{n+1}\)

a/ \(=lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\infty}=0\)
b/ \(=lim\frac{6n+1}{\sqrt{n^2+5n+1}+\sqrt{n^2-n}}=\frac{6+\frac{1}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{1}{n}}}=\frac{6}{1+1}=3\)
c/ \(=lim\frac{6n-9}{\sqrt{3n^2+2n-1}+\sqrt{3n^2-4n+8}}=lim\frac{6-\frac{9}{n}}{\sqrt{3+\frac{2}{n}-\frac{1}{n^2}}+\sqrt{3-\frac{4}{n}+\frac{8}{n^2}}}=\frac{6}{\sqrt{3}+\sqrt{3}}=\sqrt{3}\)
d/ \(=lim\frac{\left(\frac{2}{6}\right)^n+1-4\left(\frac{4}{6}\right)^n}{\left(\frac{3}{6}\right)^n+6}=\frac{1}{6}\)
e/ \(=lim\frac{\left(\frac{3}{5}\right)^n-\left(\frac{4}{5}\right)^n+1}{\left(\frac{3}{5}\right)^n+\left(\frac{4}{5}\right)^n-1}=\frac{1}{-1}=-1\)
f/ Ta có công thức:
\(1+3+...+\left(2n+1\right)^2=\left(n+1\right)^2\)
\(\Rightarrow lim\frac{1+3+...+2n+1}{3n^2+4}=lim\frac{\left(n+1\right)^2}{3n^2+4}=lim\frac{\left(1+\frac{1}{n}\right)^2}{3+\frac{4}{n^2}}=\frac{1}{3}\)
g/ \(=lim\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\right)=lim\left(1-\frac{1}{n+1}\right)=1-0=1\)
h/ Ta có: \(1^2+2^2+...+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(\Rightarrow lim\frac{n\left(n+1\right)\left(2n+1\right)}{6n\left(n+1\right)\left(n+2\right)}=lim\frac{2n+1}{6n+12}=lim\frac{2+\frac{1}{n}}{6+\frac{12}{n}}=\frac{2}{6}=\frac{1}{3}\)

a/ \(=lim\frac{\left(-\frac{2}{3}\right)^n+1}{-2.\left(-\frac{2}{3}\right)^n+3}=\frac{1}{3}\)
b/ \(=lim\frac{\left(2-\frac{1}{n}\right)\left(1+\frac{1}{n}\right)\left(3+\frac{4}{n}\right)}{\left(\frac{5}{n}-6\right)^3}=\frac{2.1.3}{\left(-6\right)^3}=-\frac{1}{36}\)
c/ \(=lim\frac{5n+3}{\sqrt{n^2+5n+1}+\sqrt{n^2-2}}=\frac{5+\frac{3}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{2}{n}}}=\frac{5}{1+1}=\frac{5}{2}\)
d/ \(=lim\frac{5.\left(\frac{1}{2}\right)^n-6}{4.\left(\frac{1}{3}\right)^n+1}=\frac{-6}{1}=-6\)
e/ \(=-n^3\left(2+\frac{3}{n}-\frac{5}{n^2}+\frac{2020}{n^3}\right)=-\infty.2=-\infty\)

Bạn muốn tìm giới hạn nhưng lại không chỉ rõ $n$ chạy đến đâu?
Điển hình như câu 1:
$n\to 0$ thì giới hạn là $3$
$n\to \pm \infty$ thì giới hạn là $\pm \infty$
Bạn phải ghi rõ đề ra chứ?

a/ \(=lim\frac{3\left(\frac{2}{7}\right)^n-8}{4.\left(\frac{3}{7}\right)^n+5}=-\frac{8}{5}\)
b/ \(=lim\frac{6.4^n-\frac{2}{9}.6^n}{\frac{1}{2}.6^n+4.3^n}=lim\frac{6\left(\frac{4}{6}\right)^n-\frac{2}{9}}{\frac{1}{2}+4.\left(\frac{3}{6}\right)^n}=\frac{-\frac{2}{9}}{\frac{1}{2}}=-\frac{4}{9}\)
c/ \(=lim\frac{\left(-\frac{3}{5}\right)^n+2}{\left(\frac{1}{5}\right)^n-1}=\frac{2}{-1}=-2\)
d/ \(=lim\frac{n\left(n+1\right)}{2\left(n^2+n+1\right)}=lim\frac{1+\frac{1}{n}}{2+\frac{2}{n}+\frac{2}{n^2}}=\frac{1}{2}\)

Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ giả thiết \(\Rightarrow n,k\ge2\)
Ta có:
\(\hept{\begin{cases}n^3-n-1>1,n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n^3-n-1=p^r\\n^2+n-1=p^s\end{cases}}\) trong đó \(\hept{\begin{cases}r\ge s\ge0\\r+s=k\end{cases}}\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác :
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\hept{\begin{cases}p=5\\k=2\end{cases}}\)
Vậy bộ số cần tìm là (n,k,p)=(2,2,5)

\(\lim\limits\frac{3-16.4^n}{2^n+3.4^n}=\lim\limits\frac{3\left(\frac{1}{4}\right)^n-16}{\left(\frac{2}{4}\right)^n+3}=-\frac{16}{3}\)

a) lim \(\frac{\left(2n+1\right)^2\left(n-1\right)}{\sqrt[3]{n^3+7n-2}}\)
= lim \(\left(2n+1\right)^2.\frac{\left(1-\frac{1}{n}\right)}{\sqrt[3]{1+\frac{7}{n^2}-\frac{2}{n^3}}}\)
\(=+\infty\)
b) lim \(\left(2n-1\right)\sqrt{\frac{2n^2+5}{n^4+n^2+2}}\)
= lim \(\left(2-\frac{1}{n}\right)\sqrt{\frac{2+\frac{5}{n^2}}{1+\frac{1}{n^2}+\frac{2}{n^4}}}\)
=2.2 = 4
c ) = lim \(n.\frac{n^2}{\sqrt[3]{\left(n^3+n^2\right)^2+n\sqrt[3]{n^3+n^2}+n^2}}\)
= lim \(n.\frac{1}{\sqrt[3]{\left(1+\frac{1}{n}\right)^2+\sqrt[3]{1+\frac{1}{n}}+1}}\)
\(=+\infty\)
Chọn B
Điều kiện: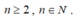
Ta có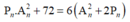
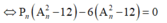
So với điều kiện, các giá trị cần tìm là n = 3; n = 4