CT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 4 2017
Bài giải:
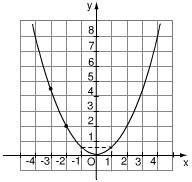
a) Theo hình vẽ, ta lấy điểm A thuộc đồ thị có tọa độ là x = -2, y = 2. Khi đó ta được:
2 = a . (-2)2 suy ra a = 
b) Đồ thị có hàm số là y = x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y = (-3)2 suy ra y = 
.
c) Các điểm thuộc parabol có tung độ là 8 là:
8 = x2 ⇔ x2 = 16 ⇔ x = ± 4
Ta được hai điểm và tọa độ của hai điểm đó là M(4; 8) và M'(-4; 8).
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Phương trình hoành độ giao điểm d và (P):
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Leftrightarrow m< -\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\Leftrightarrow m=1\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Phương trình hoành độ giao điểm:
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Rightarrow m>-\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\)
\(\Rightarrow m=1\) (thỏa mãn)
TK
29 tháng 4 2021
Vì đường thẳng (d) cắt Oy tại điểm có tung độ bằng 8
Nên m+3=8⇔ m=5
Theo pt hoành độ giao điểm của (d) và (P)
Ta có:\(x^2=2x+8\)
⇔\(x^2-2x-8=0\)
\(\Delta'=\left(-1\right)^2-\left(-8\right)=9\)
\(\sqrt{\Delta'}=\sqrt{9}=3>0\)
Vậy pt có 2 nghiệm pb
x1=\(\dfrac{1+3}{1}=4\)
x2=\(\dfrac{1-3}{1}=-2\)
Với x =4 thì y=x2=42=16
Với x =-2 thì y=x2=(-2)2=4
Vậy ......
chu vi hình chữ nhật
Điểm có tung độ bằng -8 có hoành độ thỏa mãn:
\(-2x^2=-8\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy có 2 điểm thỏa mãn là \(\left(2;-8\right)\) và \(\left(-2;-8\right)\)