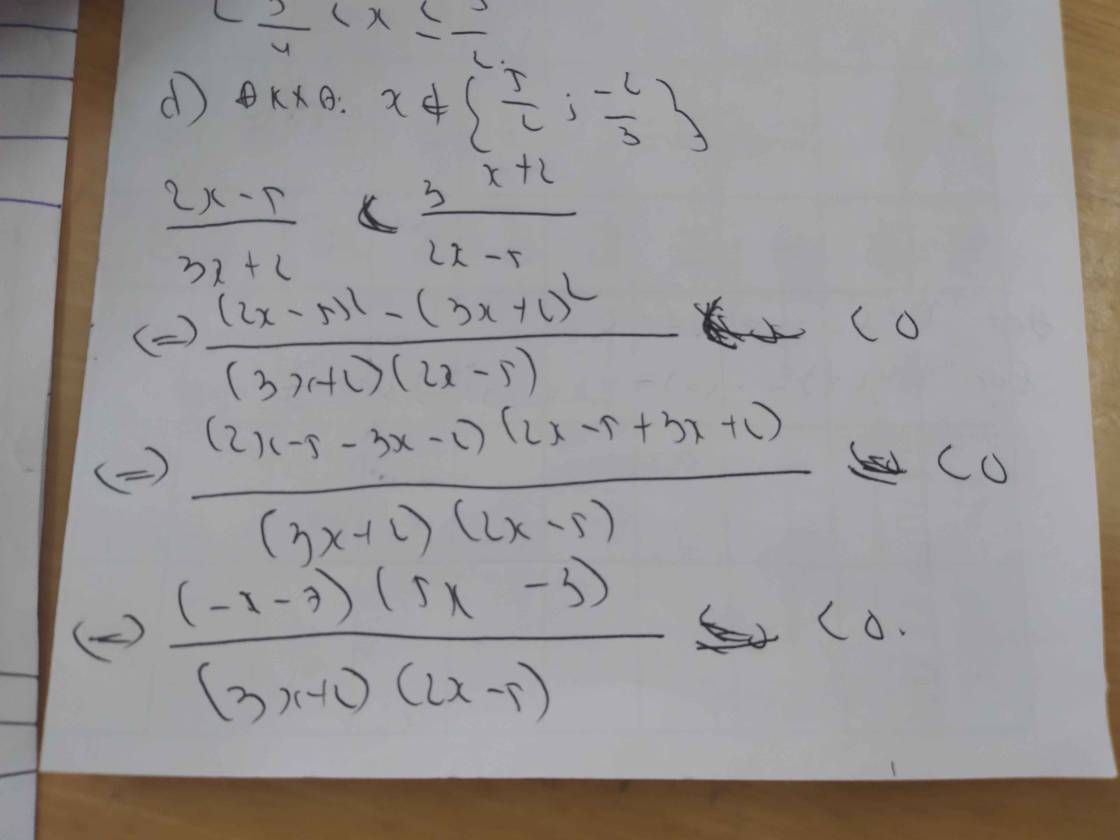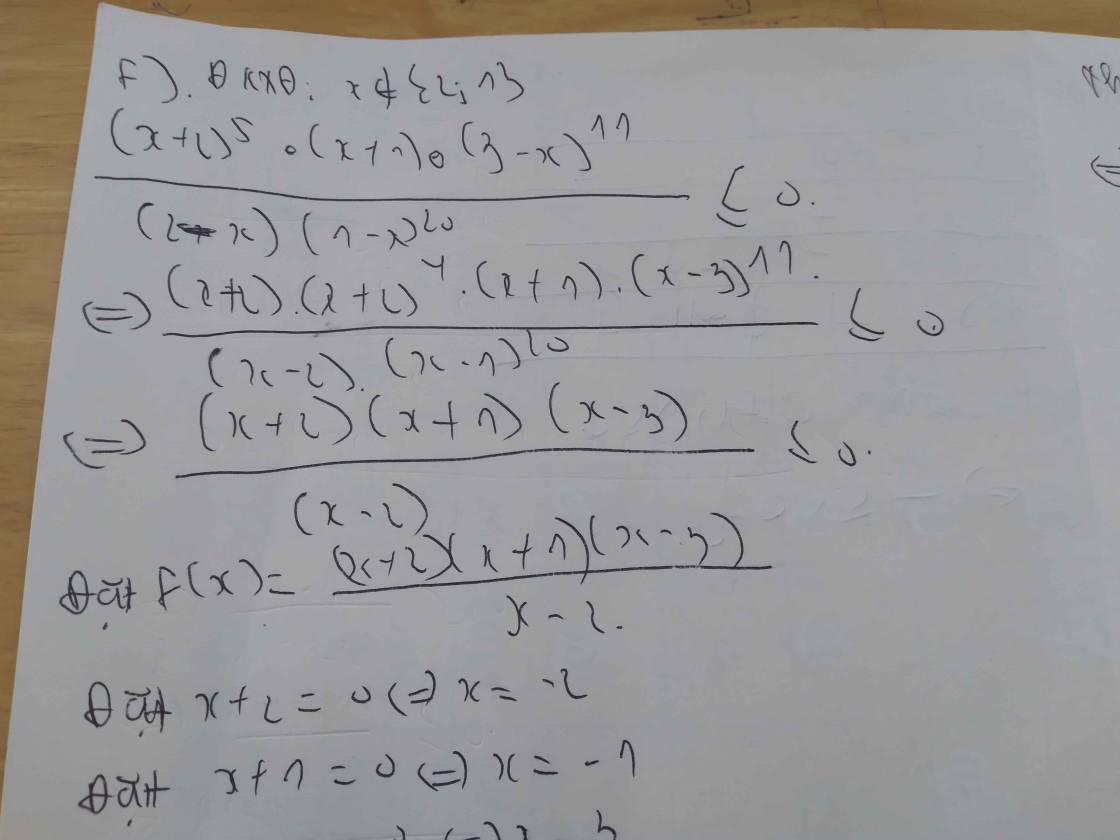Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

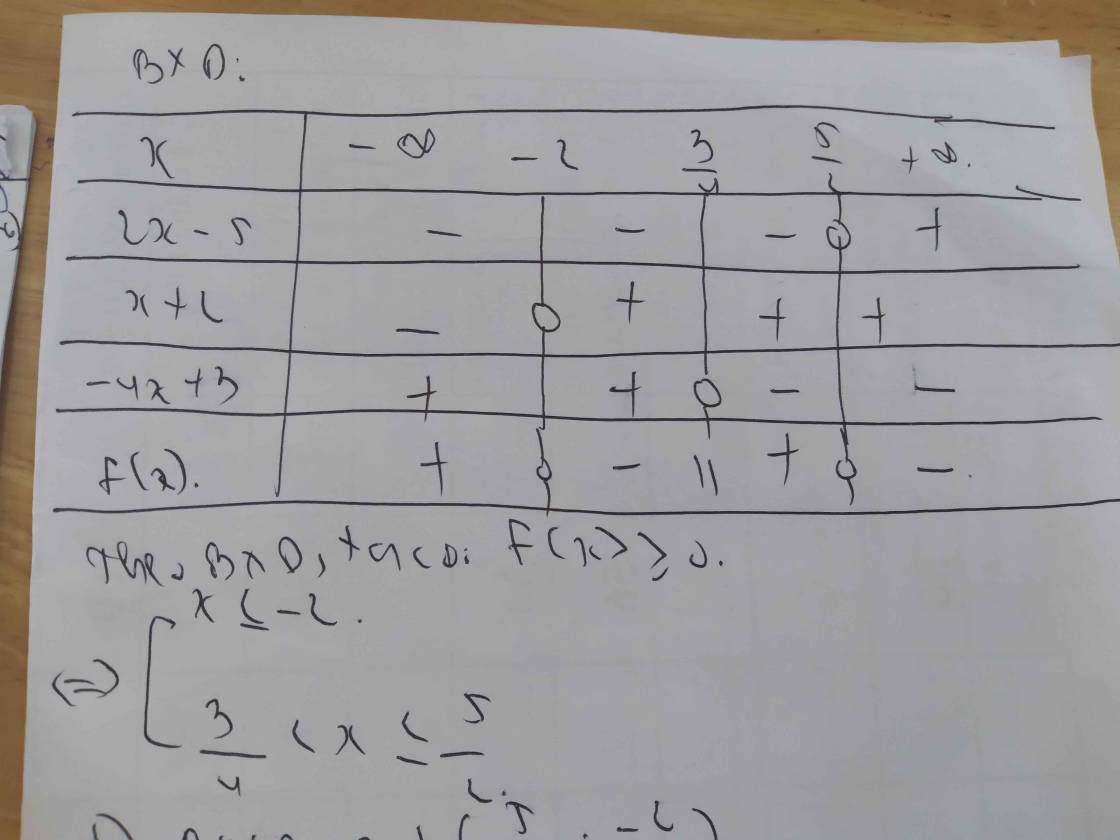
a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
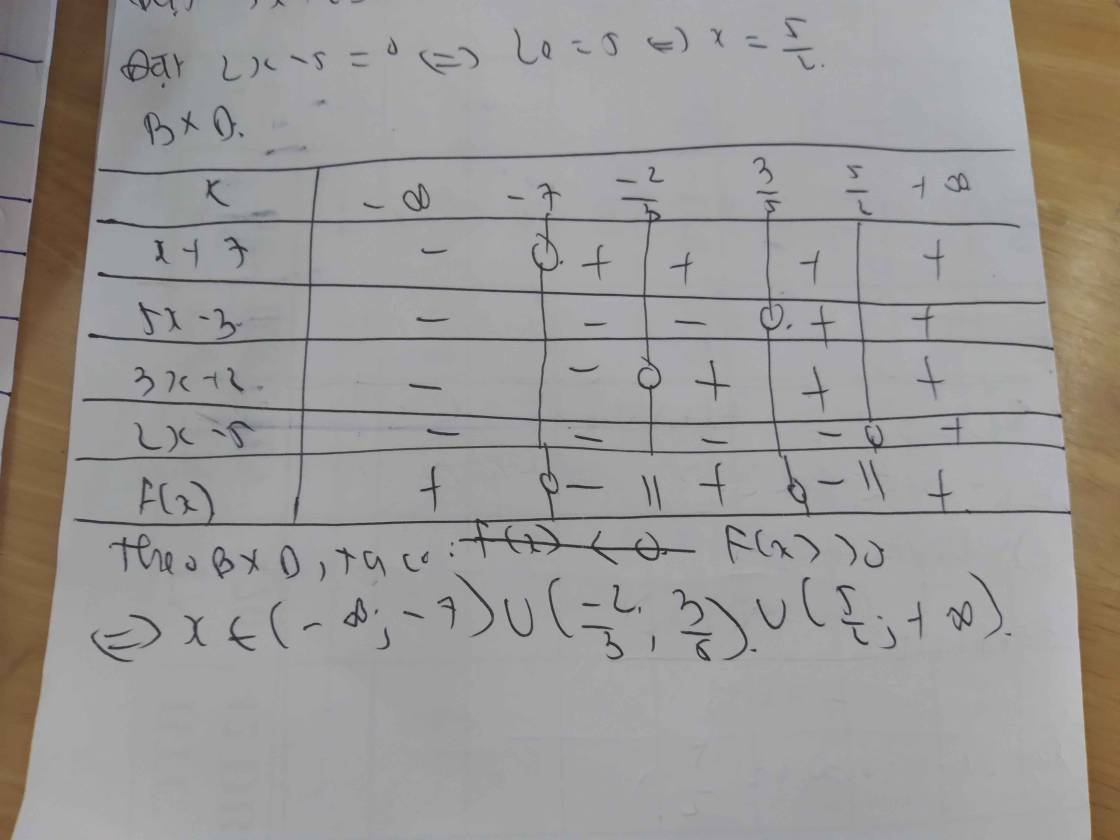
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)

a) \(\dfrac{2}{x+1}\) xác định với x≠-1, \(\sqrt{x+3}\) xác định với x ≥ -3
Tập xác định của y = là:
D = {x ∈ R/ x + 1 ≠ 0 và x + 3 ≥ 0} = [-3, +∞)\{-1}
Có thể viết cách khác: D = [-3, -1] ∪ (-1, +∞)
b) Tập xác định
D = {x ∈ R/ 2 -3x ≥ 0} ∩ {x ∈ R/ 1-2x ≥ 0}
= [-∞, 2323 ]∩(-∞, 1212) = (-∞, 1212)
c) Tập xác định là:
D = [1, +∞) ∪ (-∞,1) = R

d.
ĐKXĐ: \(x\left|x\right|-4>0\)
\(\Leftrightarrow x\left|x\right|>4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x^2>4\end{matrix}\right.\) \(\Leftrightarrow x>2\)
e.
ĐKXĐ: \(\left|x^2-2x\right|+\left|x-1\right|\ne0\)
Ta có:
\(\left|x^2-2x\right|+\left|x-1\right|=0\Leftrightarrow\left\{{}\begin{matrix}x^2-2x=0\\x-1=0\end{matrix}\right.\) (ko tồn tại x thỏa mãn)
\(\Rightarrow\) Hàm xác định với mọi x hay \(D=R\)
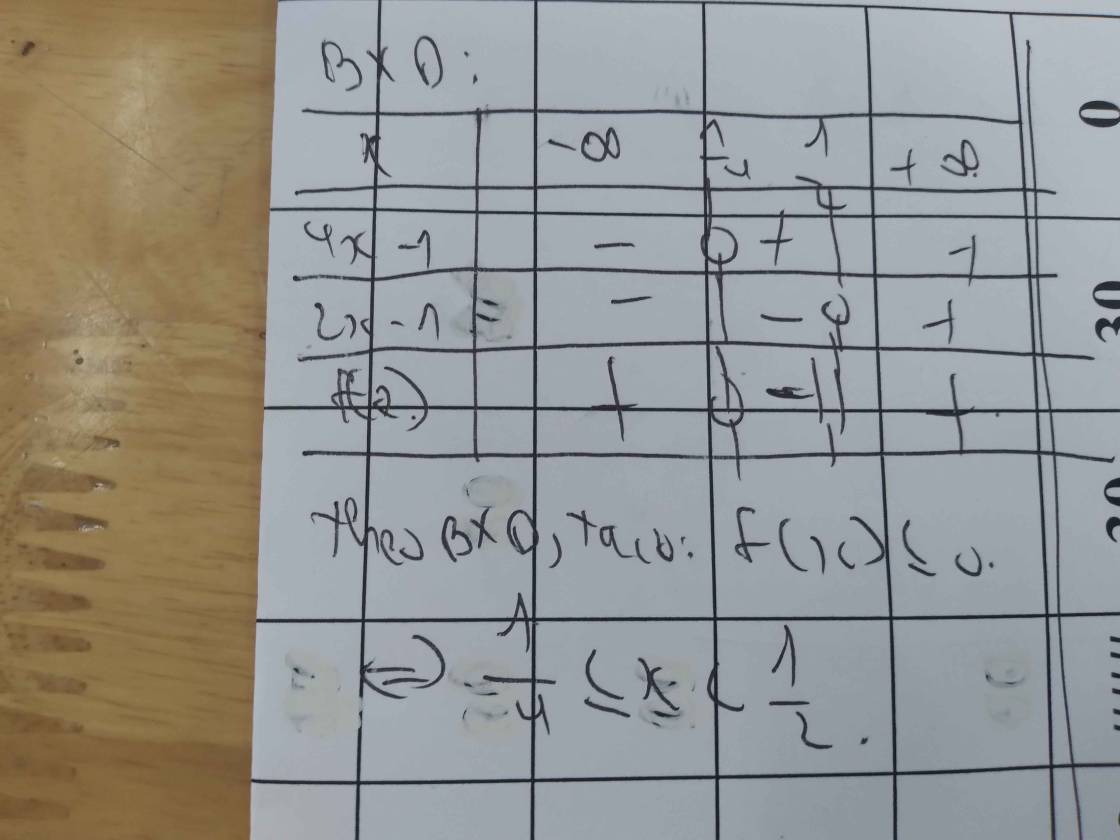
f.
ĐKXĐ: \(\left\{{}\begin{matrix}x+2\ge0\\x\left|x\right|+4\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\left|x\right|+4\ne0\end{matrix}\right.\)
Xét \(x\left|x\right|+4=0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x^2+4=0\left(vn\right)\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\-x^2+4=0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=-2\)
Hay \(x\left|x\right|+4\ne0\Leftrightarrow x\ne-2\)
Kết hợp với \(x\ge-2\Rightarrow x>-2\)

Tập nghiệm của BPT là: \(\left[{}\begin{matrix}-3< x\le-1\\0\le x< 1\\x>1\end{matrix}\right.\)

\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)

a, ĐKXĐ : \(D=R\)
BPT \(\Leftrightarrow x^2+5x+4< 5\sqrt{x^2+5x+4+24}\)
Đặt \(x^2+5x+4=a\left(a\ge-\dfrac{9}{4}\right)\)
BPTTT : \(5\sqrt{a+24}>a\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a+24\ge0\\a< 0\end{matrix}\right.\\\left\{{}\begin{matrix}a\ge0\\25\left(a+24\right)>a^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-24\le a< 0\\\left\{{}\begin{matrix}a^2-25a-600< 0\\a\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-24\le a< 0\\0\le a< 40\end{matrix}\right.\)
\(\Leftrightarrow-24\le a< 40\)
- Thay lại a vào ta được : \(\left\{{}\begin{matrix}x^2+5x-36< 0\\x^2+5x+28\ge0\end{matrix}\right.\)
\(\Leftrightarrow-9< x< 4\)
Vậy ....
b, ĐKXĐ : \(x>0\)
BĐT \(\Leftrightarrow2\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< x+\dfrac{1}{4x}+1\)
- Đặt \(\sqrt{x}+\dfrac{1}{2\sqrt{x}}=a\left(a\ge\sqrt{2}\right)\)
\(\Leftrightarrow a^2=x+\dfrac{1}{4x}+1\)
BPTTT : \(2a\le a^2\)
\(\Leftrightarrow\left[{}\begin{matrix}a\le0\\a\ge2\end{matrix}\right.\)
\(\Leftrightarrow a\ge2\)
\(\Leftrightarrow a^2\ge4\)
- Thay a vào lại BPT ta được : \(x+\dfrac{1}{4x}-3\ge0\)
\(\Leftrightarrow4x^2-12x+1\ge0\)
\(\Leftrightarrow x=(0;\dfrac{3-2\sqrt{2}}{2}]\cup[\dfrac{3+2\sqrt{2}}{2};+\infty)\)
Vậy ...