Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chia cả hai vế của bất phương trình cho 1 + a 2 x 2 + 4 x + 6 > 0 ta được:
2 a 1 + a 2 x 2 + 4 x + 6 + 1 - a 2 1 + a 2 x 2 + 4 x + 6 ≤ 1
Đặt α = tan t 2 với 0 < t 2 < π 4 ⇔ 0 < t < π 2
Khi đó 2 a 1 + a 2 = sin t và 1 - a 2 1 + a 2 = cos 2 t
Bất phương trình đã cho tương đương với
sin t x + 2 2 + 2 + cos t x + 2 2 + 2 ≤ 1
Bất phương trình (*) luôn đúng vì
sin t x + 2 2 + 2 ≤ sin 2 t và cos t x + 2 2 + 2 ≤ cos 2 t
Vậy S = R
Đáp án A

Chọn A.
Bán kính của mặt cầu S có tâm A và tiếp xúc với đường thẳng d là R = d (A,(d)).
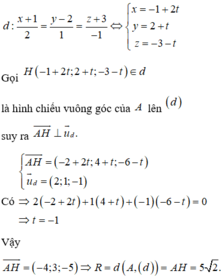

Đáp án C
Phương pháp: Cách giải phương trình log a f x = b ⇔ f x = a b 0 < a ≠ 1 ; f x > 0
Cách giải: Điều kiện: x 5 − x > 0 ⇔ 0 < x < 5
log 6 x 5 − x = 1 ⇔ x 5 − x = 6 ⇔ x 2 − 5 x + 6 = 0 ⇔ x = 2 x = 3 t m
Vậy S = 2 ; 3
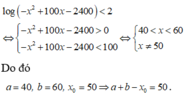
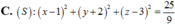

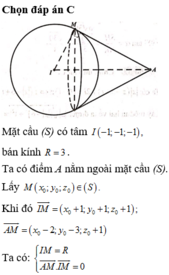

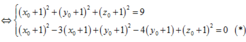
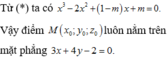

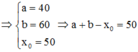
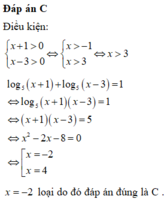

Đáp án A