K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 2 2023
e: =>2/7-x=2/5
=>7-x=5
=>x=2
f: =>2x+3/3=10/3
=>2x+3=10
=>2x=7
=>x=7/2
g: =>(14+x)/7=15/7
=>x+14=15
=>x=1
h: =>(2x+3)/x=13/x
=>2x+3=13
=>2x=10
=>x=5
CM
16 tháng 10 2019
0 : x = 0
Vì 0 chia cho một số tự nhiên bất kì khác 0 đều bằng 0.
Do đó x là các số tự nhiên khác 0 hay x ∈ N*
CM
22 tháng 11 2019
0 : x = 0.
Nhận xét: 0 chia cho một số tự nhiên bất kì khác 0 thì bằng 0.
Do đó, 0: x = 0 luôn đúng với mọi số tự nhiên x khác 0.
Hay tập hợp các số tự nhiên x thỏa mãn là: N*
NL
3
NH
11 tháng 1 2023
e)
\(\dfrac{x+2}{3}=\dfrac{3}{x+2}\\ =\left(x+2\right)^2=9\\ \left[{}\begin{matrix}x+2=3\\x+2=-3\end{matrix}\right.\\ \left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
f)
\(\dfrac{x-4}{-5}=\dfrac{-5}{x-4}\\ \left(x-4\right)^2=25\\ \left[{}\begin{matrix}x-4=5\\x-4=-5\end{matrix}\right.\\ \left[{}\begin{matrix}x=9\\x=-1\end{matrix}\right.\)
PT
1
CM
4 tháng 5 2018
a, x : 12 = 27
=> x = 27.12 = 324
Vậy x = 324
b, 1414 : x = 14
=> x = 1414 : 14 = 101
Vậy x = 101
c, 5x : 12 = 0
=> 5x = 0
=> x = 0.
Vậy x = 0
d, 0 : x = 0
∀ x ∈ ¥, x≠0
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
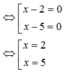
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
e) 0 : x = 0
0 chia cho mọi số tự nhiên khác 0 đều bằng 0
nên x ∈ N*