NH
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
19 tháng 12 2021
a: \(\Leftrightarrow2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2\right\}\)
26 tháng 12 2021
a,
Ta có: 4n-5 chia hết cho 2n-1
=>4n-2-3 chia hết cho 2n-1
=>2.(2n-1)-3 chia hết cho 2n-1
=>3 chia hết cho 2n-1
=>2n-1=Ư(3)=(-1,-3,1,3)
=>2n=(0,-2,2,4)
=>n=(0,-1,1,2)
Vậy n=0,-1,1,2
HP
2
2 tháng 10 2021
a) \(\Rightarrow\left(n+1\right)+5⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;4\right\}\)
b) \(\Rightarrow2\left(2n+1\right)+7⋮\left(2n+1\right)\)
\(\Rightarrow\left(2n+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;3\right\}\)
2 tháng 11 2023
Để n + 6 ⋮ n + 1 thì :
⇒ n + 1 + 5 ⋮ n + 1 mà n + 1 ⋮ n + 1
Như thế 5 ⋮ n + 1 và n + 1 ∈ Ư(5)
⇒ Ư(5)={ 1;5 }
n + 1 = 1 ⇒ n = 0
n + 1 = 5 ⇒ n = 4
Vậy .............
⋮⋮⋮
DT
3
VH
25 tháng 12 2020
Ta có: n+3 chia hết cho n-1
mà: n-1 chia hết cho n-1
suy ra:[(n+3)-(n-1)]chia hết cho n-1
(n+3-n+1)chia hết cho n-1
4 chia hết cho n-1
suy ra n-1 thuộc Ư(4)
Ư(4)={1;2;4}
suy ra n-1 thuộc {1;2;4}
Ta có bảng sau:
n-1 1 2 4
n 2 3 5
Vậy n=2 hoặc n=3 hoặc n=5
4 tháng 12 2023
Bài 10:
a: 2x-3 là bội của x+1
=>\(2x-3⋮x+1\)
=>\(2x+2-5⋮x+1\)
=>\(-5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: x-2 là ước của 3x-2
=>\(3x-2⋮x-2\)
=>\(3x-6+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\inƯ\left(4\right)\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Bài 14:
a: \(4n-5⋮2n-1\)
=>\(4n-2-3⋮2n-1\)
=>\(-3⋮2n-1\)
=>\(2n-1\inƯ\left(-3\right)\)
=>\(2n-1\in\left\{1;-1;3;-3\right\}\)
=>\(2n\in\left\{2;0;4;-2\right\}\)
=>\(n\in\left\{1;0;2;-1\right\}\)
mà n>=0
nên \(n\in\left\{1;0;2\right\}\)
b: \(n^2+3n+1⋮n+1\)
=>\(n^2+n+2n+2-1⋮n+1\)
=>\(n\left(n+1\right)+2\left(n+1\right)-1⋮n+1\)
=>\(-1⋮n+1\)
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)
mà n là số tự nhiên
nên n=0
28 tháng 10 2021
a) \(\left(n+6\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+5⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;4\right\}\)
b) \(\left(4n+9\right)⋮\left(2n+1\right)\Rightarrow2\left(2n+1\right)+7⋮\left(2n+1\right)\)
\(\Rightarrow\left(2n+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;3\right\}\)
7 tháng 10 2021
a: \(n\in\left\{1;7\right\}\)
b: \(n-1\in\left\{-1;1;7\right\}\)
hay \(n\in\left\{0;2;8\right\}\)
c: \(2n-1\in\left\{-1;1;7\right\}\)
\(\Leftrightarrow2n\in\left\{0;2;8\right\}\)
hay \(n\in\left\{0;1;4\right\}\)
24 tháng 9 2021
\(a,\Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ b,\Rightarrow n+3+5⋮n+3\\ \Rightarrow5⋮n+3\\ \Rightarrow n+3\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Rightarrow n\in\left\{-8;-4;-2;2\right\}\\ c,\Rightarrow2\left(2n-1\right)-3⋮2n-1\\ \Rightarrow3⋮2n-1\\ \Rightarrow2n-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Rightarrow n\in\left\{-1;0;1;2\right\}\\ d,\Rightarrow8-n+4⋮8-n\\ \Rightarrow4⋮8-n\\ \Rightarrow8-n\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow n\in\left\{12;10;9;7;6;4\right\}\)
PN
4
24 tháng 1 2021
a) Ta có:\(n-6⋮n-1\)
\(\Leftrightarrow n-1-5⋮n-1\)
mà \(n-1⋮n-1\)
nên \(-5⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(-5\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)
Vậy: \(n\in\left\{2;0;6;-4\right\}\)
b) Ta có: \(3n+2⋮n-1\)
\(\Leftrightarrow3n-3+5⋮n-1\)
mà \(3n-3⋮n-1\)
nên \(5⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(5\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)
Vậy: \(n\in\left\{2;0;6;-4\right\}\)
c) Ta có: \(n^2+5⋮n+1\)
\(\Leftrightarrow n^2+2n+1-2n+4⋮n+1\)
\(\Leftrightarrow\left(n+1\right)^2-2n-2+6⋮n+1\)
mà \(\left(n+1\right)^2⋮n+1\)
và \(-2n-2⋮n+1\)
nên \(6⋮n+1\)
\(\Leftrightarrow n+1\inƯ\left(6\right)\)
\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
Vậy: \(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
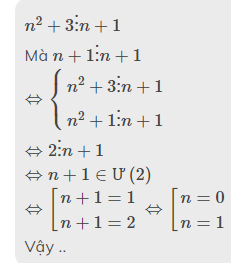
a: \(\Leftrightarrow2n-1\in\left\{-1;1;3\right\}\)
hay \(n\in\left\{0;1;2\right\}\)
câu b nữa bạn