
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Để 21n+4/14n+3 là phân số tổi giản thì ƯCLN(21n+4; 14n+3) =1
Gọi ƯCLN(21n+4; 14n+3) =d => 21n+4 \(⋮\)d; 14n+3 \(⋮\)d
=> (14n+3) -(21n+4) \(⋮\)d
=> 3(14n+3) -2(21n+4) \(⋮\)d
=> 42n+9 - 42n -8 \(⋮\)d
=> 1\(⋮\)d
=> 21n+4/14n+3 là phân số tối giản
Vậy...
c) Gọi ƯC(21n+3; 6n+4) =d; 21n+3/6n+4 =A => 21n+3 \(⋮\)d; 6n+4 \(⋮\)d
=> (6n+4) - (21n+3) \(⋮\)d
=> 7(6n+4) - 2(21n+3) \(⋮\)d
=> 42n +28 - 42n -6\(⋮\)d
=> 22 \(⋮\)cho số nguyên tố d
d \(\in\){11;2}
Nếu phân số A rút gọn được cho số nguyên tố d thì d=2 hoặc d=11
Nếu A có thể rút gọn cho 2 thì 6n+4 luôn luôn chia hết cho 2. 21n+3 chia hết cho 2 nếu n là số lẻ
Nếu A có thể rút gọn cho 11 thì 21n+3 \(⋮\)11 => 22n -n +3\(⋮\)11 => n-3 \(⋮\)11 Đảo lại với n=11k+3 thì 21n+3 và 6n+4 chia hết cho 11
Vậy với n là lẻ hoặc n là chẵn mà n=11k+3 thì phân số đó rút gọn được

Vì 12n+1 = 12n +24 - 23 = 12 (n+2) - 23
=> 12n+1 / 2 (n+2) = 12 (n+2) - 23 / 2n (n+2) = 12 (n+2) / 2n (n+2) - 23 / 2n (n+2) = 6 / n - 23 / 2n (n+2)
Ta có: 2n (n+2) chia hết cho 2
=> 2n (n+2) là số chẵn
Mà 23 là số lẻ nên phân số 23 / 2n (n+2) là phân số tối giản
=> 6 / n - 23 / 2n (n+2) là phân số tối giản
Vậy 12n+1 / 2 (n+2) là phân số tối giản

Sau một hồi tìm hiểu thì mình đã có lời giải r, bạn nào chưa bt thì tham khảo nhé !
Vì 12n+1 = 12n +24 - 23 = 12 (n+2) - 23
=> 12n+1 / 2 (n+2) = 12 (n+2) - 23 / 2n (n+2) = 12 (n+2) / 2n (n+2) - 23 / 2n (n+2) = 6 / n - 23 / 2n (n+2)
Ta có: 2n (n+2) chia hết cho 2
=> 2n (n+2) là số chẵn
Mà 23 là số lẻ nên phân số 23 / 2n (n+2) là phân số tối giản
=> 6 / n - 23 / 2n (n+2) là phân số tối giản
Vậy 12n+1 / 2 (n+2) là phân số tối giản

1. Để A tối giản thì:
(n + 1, n + 3) = 1
Gọi d là ƯC nguyên tố của n + 1 và n + 3
=> n + 3 - n - 1 chia hết cho d
=> 2 chia hết cho d
Mà d nguyên tố
=> d = 2
Tìm n để n + 1 chia hết cho d; n + 3 chia hết cho 2
Vì n + 3 = n + 1 + 2 nên n + 3 chia hết cho 2 thì n + 1 chia hết cho 2
=> n + 3 = 2k (k thuộc Z)
=> n = 2k - 3
Vậy n khác 2k - 3 thì A tối giản.
2. 12n + 1 / 30n + 2 tối giản
=> (12n + 1, 30n + 2) = 1
Gọi ƯCLN (12n + 1, 30n + 2) = d
=> 12n + 1 chia hết cho d => 5.(12n + 1) = 60n + 5 chia hết cho d
=> 30n + 2 chia hết cho d => 2.(30n + 2) = 60n + 4 chia hết cho d
=> 60n + 5 - 60n - 4 chia hết cho d
=> 1 chia hết cho d
=> d = 1
Vậy p/số trên tối giản.
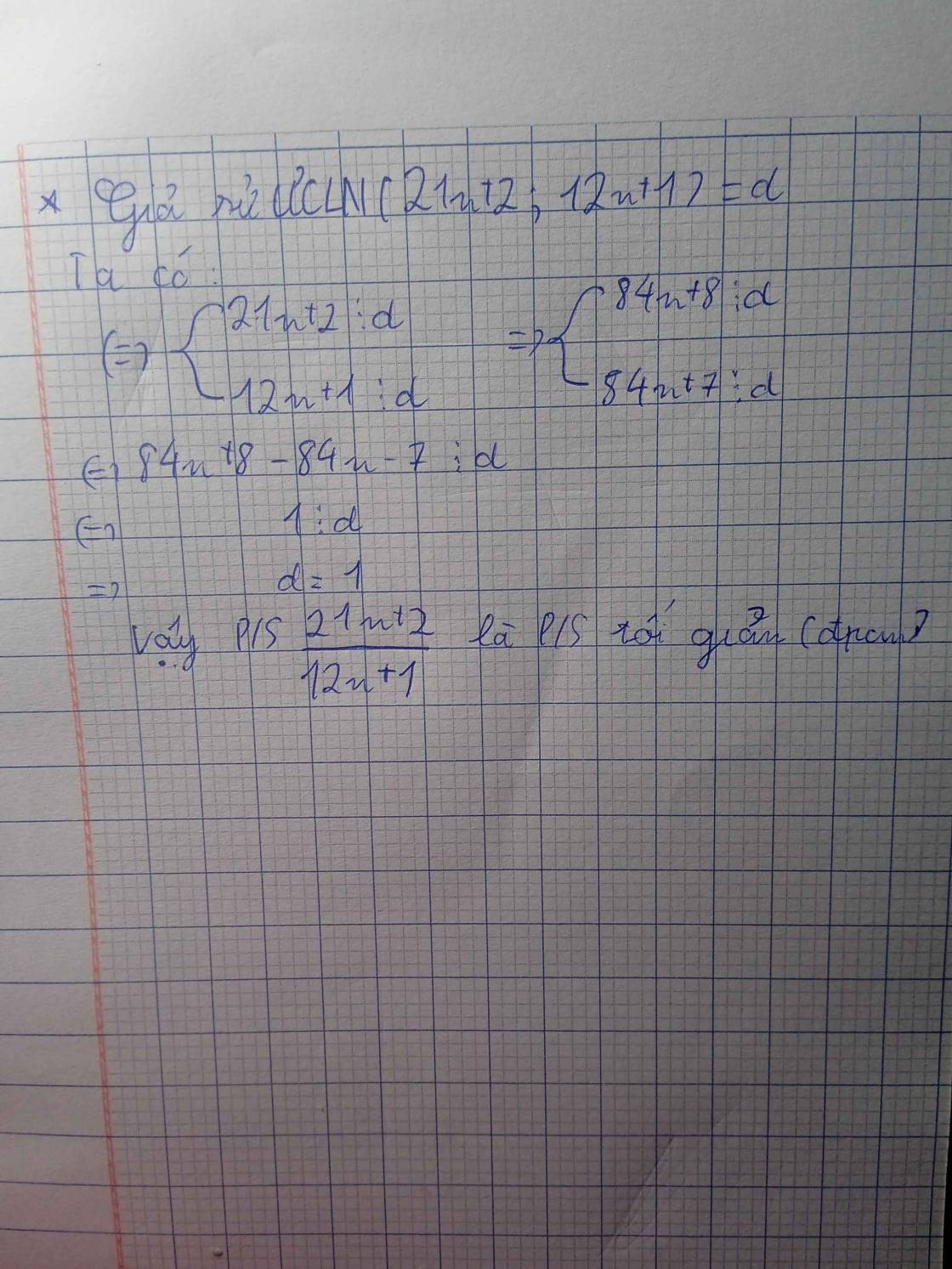
giúp mình với vì thời gian có hạn