
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

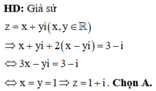

a)A=x+3/x-2
A=x-2+5/x-2
A=1+5/x-2
vì 1 thuộc Z nên để A thuộc Z thì 5 phải chia hết cho x-2
x-2 thuộc ước của 5
x-2 thuộc -5;-1;1;5
x = -3;1;3 hoặc 7
giá trị các biểu thức theo giá trị của x như trên và lần lượt là 0;-4;6;2
b)để B= 1-2x/2+x thuộc Z thì
1-2x phải chia hết cho 2+x
nên 1-2x-4+4 phải chia hết cho x+2
1-(2x+4)+4 phải chia hết cho x+2
1+4-[2(x+2] phải chia hết cho x+2
5 -[2(x+2] phải chia hết cho x+2
vì [2(x+2] chia hết cho x+2 nên 5 phải chia hết cho x+2
suy ra x+2 thuộc ước của 5
x+2 thuộc -5;-1;1;5
x=-7;-3;-1;3
giá trị các biểu thức theo giá trị của x như trên và lần lượt là -3;-7;3;-1

2x3-1=15=>x3=(15+1):2=16:2=8
=>x=2
Thay x=2 vào ta được :
(y-15)/16=(z+9)/25=18/9=2
(*) (y-15)/16=2=>y-15=2.16=32=>y=47
(*) (z+9)/25=2=>z+9=50=>z=41
Vậy (x;y;z)=(2;47;41)

b,(*)chứng minh a=-3b:
xét a-b=2(a+b)
=>a-b=2a+2b
=>-b-2b=2a-a
=>-3b=a (đpcm)
(*) tính a/b :
Từ -3b=a=>a/b=-3
(*)tính a và b:
Ta có : a-b=a/b=-3
và 2(a+b)=a/b=-3
hệ pt<=>a-b=-3
và 2(a+b)=-3
<=>a-b=-3 (1)
và a+b=-1,5 (2)
Lấy (1)+(2),vế theo vế ta đc:
(a-b)+(a+b)=-3+(-1,5)
=>a-b+a+b=-4,5
=>2a=-4,5=>a=-2,25
Mà a-b=-3=>b=0,75
Vậy (a;b)=(-2,25;0,75)
c) vì (x-y2+z)2 >= 0 với mọi x;y;z
(y-2)2 >= 0 với mọi y
(z+3)2 >= 0 với mọi z
=>(x-y2+z)2+(y-2)2+(z+3)2 >= 0 với mọi x;y;z
Mà theo đề: (x-y2+z)2+(y-2)2+(z+3)2=0
=>(x-y2+z)2=(y-2)2=(z+3)2=0
+)(y-2)2=0=>y=2
+)(z+3)2=0=>z=-3
Thay y=2;z=-3 vào (x-y2+z)2=0=>x-22+(-3)2=0=>x=-5
Vậy (x;y;z)=(-5;2;-3)

ta có 3n+2 chia hết cho 2n+1
Nên 2(3n+2) chia hết cho 2n+1
6n+4 chia hết cho 2n+1
6n+3+1 chia hết cho 2n+1
(6n+3)+1 chia hết cho 2n+1
3*(2n+1)+1 chia hết cho 2n+1
Mà 3*(2n+1) chia hết cho 2n+1 nên 1 phải chia hết cho 2n+1
Nên 2n+1E Ư(1)
2n+1E{1;-1}
Nếu 2n+1=1
2n=1-1
2n=0
n=0
Nếu 2n+1=-1
2n=-1-1
2n=-2
n=-1
KL: vậy n=-1 hoặc n=0

3(x-2)-4(2x+1)-5(2x+3)=50
<=>(3x-6)-(8x+4)-(10x+15)=50
<=>3x-6-8x-4-10x-15=50
<=>(3x-8x-10x)+(-6-4-15)=50
<=>-15x-25=50
<=>-15x=75
<=>x=-5
\(3\frac{1}{2}:\left(4-\frac{1}{3}\left|2x+1\right|\right)=\frac{21}{22}\)
<=>\(4-\frac{1}{3}\left|2x+1\right|=\frac{7}{2}:\frac{21}{22}=\frac{11}{3}\)
<=>\(\frac{1}{3}\left|2x+1\right|=4-\frac{11}{3}=\frac{1}{3}\)
<=>\(\left|2x+1\right|=1\)
<=>2x+1=1 hoặc 2x+1=-1
<=>2x=0 hoặc 2x=-2
<=>x=0 hoặc x=-2
Vậy......................

Theo hệ quả của bất đẳng thức Cauchy - Schwarz
\(\Rightarrow x^2+y^2+z^2\ge xy+yz+xz\)
Mà \(x^2+y^2+z^2\le3\)
\(\Rightarrow xy+yz+xz\le3\)
Ta có \(P=\dfrac{1}{1+xy}+\dfrac{1}{1+yz}+\dfrac{1}{1+xz}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow P\ge\dfrac{\left(1+1+1\right)^2}{xy+1+yz+1+xz+1}=\dfrac{9}{xy+yz+xz+3}\) (1)
Ta có \(xy+yz+xz\le3\)
\(\Rightarrow xy+yz+xz+3\le6\)
\(\Rightarrow\dfrac{9}{xy+yz+xz+3}\ge\dfrac{9}{6}=\dfrac{3}{2}\) (2)
Từ (1) và (2)
\(\Rightarrow P\ge\dfrac{3}{2}\)
Vậy \(P_{min}=\dfrac{3}{2}\)
Dấu " = " xảy ra khi \(x=y=z=1\)