
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\Leftrightarrow2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2;-1\right\}\)
c: \(\Leftrightarrow n+1\in\left\{1;-1\right\}\)
hay \(n\in\left\{0;-2\right\}\)

`4n+3 vdots 2n+1`
`=>4n+2+1 vdots 2n+1`
`=>2(2n+1)+1 vdots 2n+1`
`=>1 vdots 2n+1`
`=>2n+1 in Ư(1)={1,-1}`
`*2n+1=1=>2n=0=>n=0(tm)`
`*2n+1=-1=>2n=-2=>n=-1(tm)`
Vậy `n in {0;-1}` thì `4n+3 vdots 2n+1`
\(4n+3⋮2n+1\Leftrightarrow2\left(2n+1\right)+1⋮2n+1\Leftrightarrow1⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(1\right)=\left\{\pm1\right\}\)
| 2n + 1 | 1 | -1 |
| n | 0 | -1 |

4n+1 hia hết cho 2n-1
=>4n-2+3 chia hết cho 2n-1
2(2n-1)+3 chia hết cho2n-1 mà 2(2n-1) chia hết cho 2n-1 nên 3 chia hết cho 2n-1
hay 2n-1 thuộc Ư(3)={3;-3;1;-1}
2n-1=3=>n=2
2n-1=-3=>n=-1
2n-1=1=>n=1
2n-1=-1=>n=0
VẬY n thuộc {2;-1;1;0}
Theo bài ra ta có:
4n+1chia hết cho 2n-1
=>(4n+1)-(2n-1)chia hết cho2n-1
=>(4n+1)-2.(2n-1) chia hết cho 2n-1
=>4n+1-4n-2 chia hết cho 2n-1
=>-1 chi hết cho 2n-1=>2n-1 thuộc Ư(-1)={1;-1}
| 2n-1 | 1 | -1 |
| n | 1 | 0 |
Vậy n=1 hoặc n=0

\(a,\left(n+5\right)⋮\left(n+2\right)\)
\(\left(n+2+3\right)⋮\left(n+2\right)\)
\(\Rightarrow3⋮\left(n+2\right)\)
\(\Rightarrow n+2\in\left(1;-1;3;-3\right)\)
\(\Rightarrow n\in\left(-1;-3;1;-5\right)\)
b,c,d Tự làm
* Do p > 3 , mà một số > 3 khi chia cho 3 có hai trường hợp xảy ra : 3k + 1 ; 3k + 2.(k thuộc N)(ko lấy 3k vì 3k là hợp số)
Với p = 3k + 1
=> p + 8 = 3k + 1 + 8 = 3k + 9 ko phải là SNT
Với p = 3k + 2
=> p + 8 = 3k + 10 là SNT
=> p + 100 = 3k + 2 + 100 = 3k + 102 là hợp số .
Vậy p + 100 là hợp số

4n-9 = 4n+2-11 = 2(2n+1)-11. Nhận thấy: 2(2n+1) chia hết cho 2n+1 với mọi n
=> Để (4n-9) chia hết cho 2n+1 thì 11 phải chia hết cho 2n+1
=> 2n+1 = (-11,-1,1,11)
| 2n+1 | -11 | -1 | 1 | 11 |
| n | -6 | -1 | 0 | 5 |

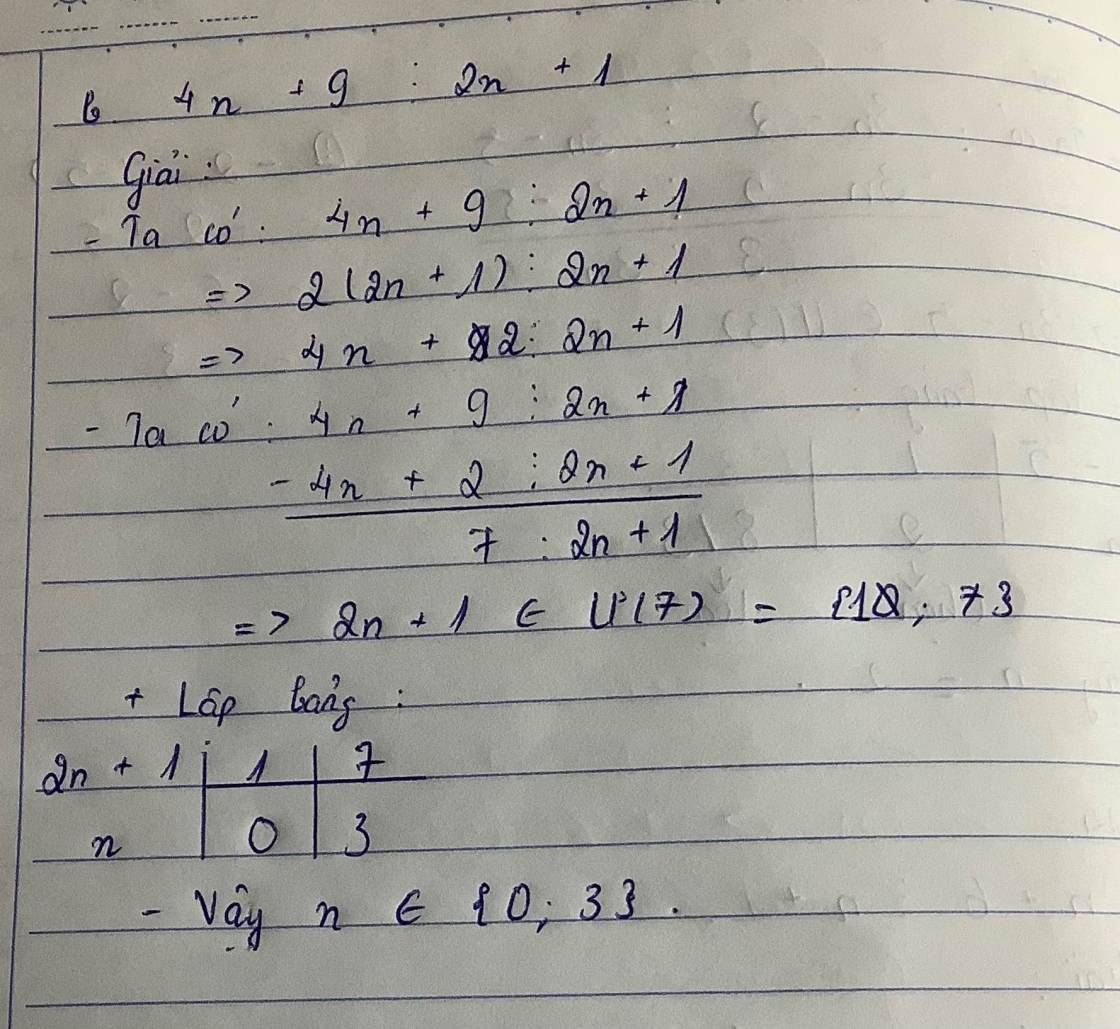
\(\left(4n+1\right)⋮\left(2n-1\right)\\ \Rightarrow\left(4n-2+3\right)⋮\left(2n-1\right)\\ \Rightarrow\left[2\left(2n-1\right)+3\right]⋮\left(2n-1\right)\)
Vì \(2\left(2n-1\right)⋮\left(2n-1\right)\Rightarrow3⋮\left(2n-1\right)\Rightarrow2n-1\inƯ\left(3\right)\)
Ta có bảng:
Vậy \(n\in\left\{-1;0;1;2\right\}\)