
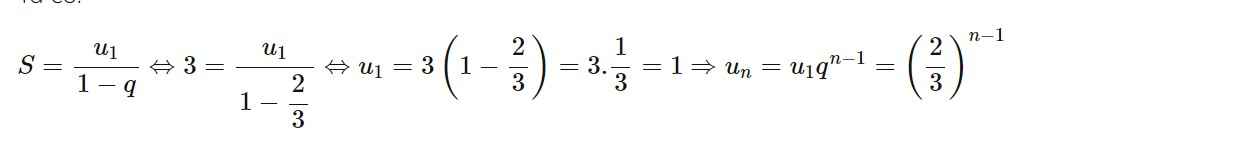
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

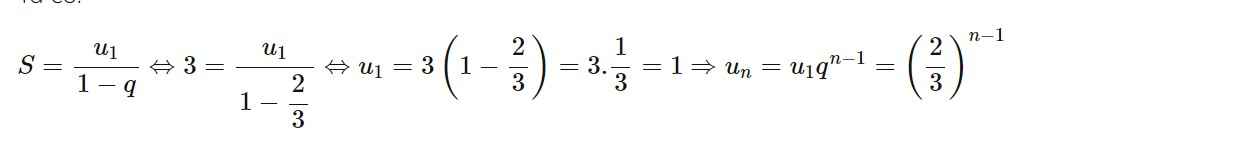

a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
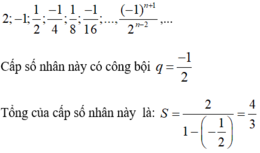


Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 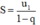

a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3

\(\dfrac{u_1}{1-q}=2\Rightarrow q=\dfrac{2-u_1}{2}\)
\(u_1+u_1q+u_1q^2=\dfrac{9}{4}\)
\(\Rightarrow u_1+\dfrac{u_1\left(2-u_1\right)}{2}+\dfrac{u_1\left(2-u_1\right)^2}{4}=\dfrac{9}{4}\)
\(\Rightarrow u_1^3-6u_1^2+12u_1-9=0\)
\(\Rightarrow u_1=3\)

a) \({u_1} = 5,\;\;{u_2} = 10,\;\;\;{u_3} = 15,\;\;{u_4} = 20,\;\;\;{u_5} = 25\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{5n}}{{5n - 1}} \)phụ thuộc vào n.
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
b) \({u_1} = 5,\;\;{u_2} = 25,\;\;{u_3} = 125,\;\;\;{u_4} = 625,\;\;\;{u_5} = 3125\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{{5^n}}}{{{5^{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = 5 \times {5^{n - 1}}= 5^{n}\).
c) \({u_1} = 1,\;\;\;{u_2} = 2,\;\;\;{u_3} = 6,\;\;\;{u_4} = 24,\;\;\;{u_5} = 120\).
có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = n\) phụ thuộc vào n, \(\forall n \in {N^*}\).
Suy ra dãy số \(\left( {{u_n}} \right)\) không phải là cấp số nhân.
d) \({u_1} = 1,\;\;{u_2} = 5,\;\;{u_3} = 25,\;\;\;{u_4} = 125,\;\;\;{u_5} = 625\).
Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = 5,\;\forall n \ge 2\).
Do đó dãy số \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 5\).
Số hạng tổng quát: \({u_n} = {5^{n - 1}}\).

Chọn C
Gọi q là công bội của cấp số. Khi đó ta có
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
⇔ u 2 + u 3 + u 4 = 39 11 u 1 + u 5 = 82 11 ⇔ u 1 q + q 2 + q 3 = 39 11 u 1 1 + q 4 = 82 11
Suy ra:
q 4 + 1 q 3 + q 2 + q = 82 39 ⇔ 39 q 4 − 82 q 3 − 82 q 2 − 82 q + 39 = 0
⇔ ( 3 q − 1 ) ( q − 3 ) ( 13 q 2 + 16 q + 13 ) = 0 ⇔ q = 1 3 , q = 3
q = 1 3 ⇒ u 1 = 81 11 ⇒ u n = 81 11 . 1 3 n − 1
q = 3 ⇒ u 1 = 1 11 ⇒ u n = 3 n − 1 11