Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

Ta có : u3 = u1 + 2d ;
u5 = u1 + 4d ;
u6 = u1 + 5d
Theo đề bài ta có :
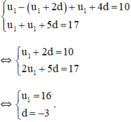

a) \(\left\{{}\begin{matrix}u_2-u_3+u_5=10\\u_4+u_6=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+d-u_1-2d+u_1+4d=10\\u_1+3d+u_1+5d=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+3d=10\\2u_1+8d=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}u_2-u_6+u_4=-7\\u_8-2u_7=2u_4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+d-u_1-5d+u_1+3d=-7\\u_1+7d-2\left(u_1+6d\right)=2\left(u_1+3d\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1-d=-7\\-3u_1-11d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=\dfrac{-11}{2}\\d=\dfrac{3}{2}\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}u_7-u_3=8\\u_2.u_7=75\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+6d-u_1-2d=8\\\left(u_1+d\right)\left(u_1+6d\right)=75\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4d=8\\\left(u_1+d\right)\left(u_1+6d\right)=75\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=2\\\left(u_1+2\right)\left(u_1+12\right)=75\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=2\\u_1^2+14u_1+24=75\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=2\\\left[{}\begin{matrix}u_1=3\\u_1=-17\end{matrix}\right.\end{matrix}\right.\)

a) Dãy số trên là cấp số cộng
Ta có:
\(\begin{array}{l}{u_n} = {u_1} + \left( {n - 1} \right)d \Rightarrow {u_1} + \left( {n - 1} \right)d = 3 - 2n\\ \Leftrightarrow {u_1} + nd - d = 3 - 2n\\ \Leftrightarrow \left\{ \begin{array}{l}{u_1} - d = 3\\nd = - 2n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\d = - 2\end{array} \right.\end{array}\)
b) Dãy số trên là cấp số cộng
Ta có:
\(\begin{array}{l}{u_n} = {u_1} + \left( {n - 1} \right)d \Rightarrow {u_1} + \left( {n - 1} \right)d = \frac{{3n + 7}}{5}\\ \Leftrightarrow {u_1} + nd - d = \frac{{3n}}{5} + \frac{7}{5}\\ \Leftrightarrow \left\{ \begin{array}{l}{u_1} - d = \frac{7}{5}\\nd = \frac{3}{5}n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 2\\d = \frac{3}{5}\end{array} \right.\end{array}\)
c) Dãy số đã cho không là cấp số cộng
Ta có: \( u_{n+1} = 3^{n+1} = 3.3^n \)
Xét hiệu \( u_{n+1} – u_n = 3.3^n – 3^n = 2.3^n \) với n ∈ ℕ*

1, Dãy a nha với d= 2
2,
\(u_1=3.1+1=4\\ u_2=3.2+1=7\\ d=u_2-u_1=7-4=3\)

Chọn C
- Theo đầu bài ta có: u 1 = - 15 ; u 8 = 69 .
- Ta có:
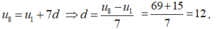

\(\left\{{}\begin{matrix}S_{15}=585\\u_1^3+\left(u_2\right)^3=302094\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}15\cdot\dfrac{2\cdot u_1+14d}{2}=585\\u_1^3+\left(u_1+d\right)^3=302094\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+7d=39\\u_1^3+\left(u_1+d\right)^3=302094\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1=39-7d\\\left(39-7d\right)^3+\left(39-7d+d\right)^3=302094\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1=39-7d\\59319-31941d^2+5733d-343d^3+59319-18252d^2+2808d-216d^3=302094\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1=39-7d\\118638-50193d+8541d^2-559d^3=302094\end{matrix}\right.\)
=>d=-2,46(loại)
Vậy: Không có bộ số số hạng đầu và công sai nào thỏa mãn đề bài

\(\left\{{}\begin{matrix}u2-3u8=-20\\u_3\cdot u_4=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1+d-3\left(u1+7d\right)=-20\\u3\cdot u4=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2u1-20d=-20\\u3\cdot u4=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1+10d=10\\\left(u1+2d\right)\cdot\left(u1+3d\right)=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1=10-10d\\\left(10-10d+2d\right)\left(10-10d+3d\right)=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1=10-10d\\\left(-8d+10\right)\left(-7d+10\right)=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1=10-10d\\56d^2-150d+126=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}d\in\varnothing\\u1=10-10d\end{matrix}\right.\)
=>Không có số hạng đầu và công sai nào thỏa mãn yêu cầu đề bài

Ta có: u7 = u1 + 6d ; u3 = u1 + 2d ; u2 = u1 + d
Do đó theo đề bài ta có: