
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Góc đối đỉnh của \(\widehat {yOv}\) là \(\widehat {zOu}\) vì tia Oz đối tia Oy, Ou đối tia Ov
b) Ta có: \(\widehat {uOz} = \widehat {yOv}\) ( 2 góc đối đỉnh), mà \(\widehat {yOv} = 110^\circ \) nên \(\widehat {uOz} = 110^\circ \)

a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)

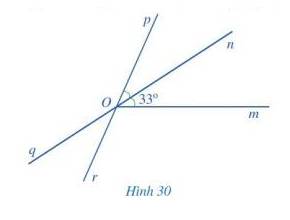
Vì On là tia phân giác của \(\widehat {mOp}\) nên:
+) \(\widehat {pOn}= \widehat {mOn}=33^\circ \)
+) \(\widehat {mOp} = 2.\widehat {mOn} = 2.33^\circ = 66^\circ \)
Vì \(\widehat {qOr} = \widehat {pOn}\) ( 2 góc đối đỉnh), mà \(\widehat {pOn} = 33^\circ \Rightarrow \widehat {qOr} = 33^\circ \)
Vì \(\widehat {pOq} + \widehat {qOr} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {pOq} + 33^\circ = 180^\circ \Rightarrow \widehat {pOq} = 180^\circ - 33^\circ = 147^\circ \)
Vậy \(\widehat {mOp} = 66^\circ ;\widehat {qOr} = 33^\circ ;\widehat {pOq} = 147^\circ \)

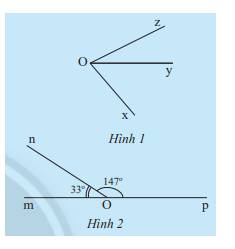
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)

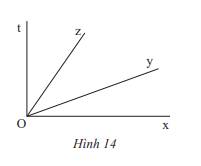
a) Các góc kề với \(\widehat {xOy}\) là: \(\widehat {yOz};\widehat {yOt}\)
b) Ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\\ \Rightarrow 20^\circ + \widehat {zOt} + \widehat {zOt} = 90^\circ \\ \Rightarrow 2.\widehat {zOt} = 90^\circ - 20^\circ = 70^\circ \\ \Rightarrow \widehat {zOt} = 70^\circ :2 = 35^\circ \end{array}\)

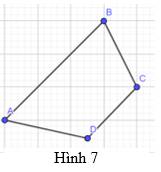
Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC
\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC = \({180^o}\)
\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\)

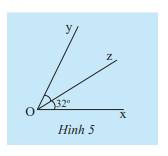
Vì tia Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy}\) và \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\)
Như vậy, \(\widehat {yOz} = \widehat {xOz} = 32^\circ \) nên \(\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\) = \(32^\circ + 32^\circ = 64^\circ \)
Chú ý:
Nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)

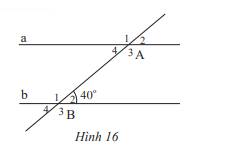
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)

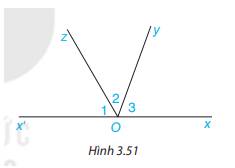
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)
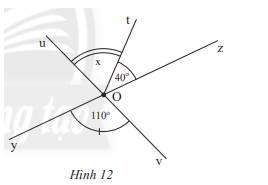
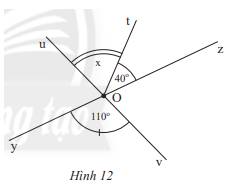
Ta có: \(\widehat {uOz} = \widehat {yOv}\) ( 2 góc đối đỉnh), mà \(\widehat {yOv} = 110^\circ \) nên \(\widehat {uOz} = 110^\circ \)
Mà \(\widehat {uOt},\widehat {tOz}\) là 2 góc kề nhau nên \(\widehat {uOt} + \widehat {tOz} = \widehat {uOz}\)
\(\begin{array}{l} \Rightarrow x + 40^\circ = 110^\circ \\ \Rightarrow x = 110^\circ - 40^\circ = 70^\circ \end{array}\)
Vậy x = 70\(^\circ \)