Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt hoành độ giao điểm:
\(-x^2+2x+3=-2x+1\)
\(\Leftrightarrow x^2-4x-2=0\Rightarrow\left[{}\begin{matrix}x=2+\sqrt{6}\Rightarrow y=-3-2\sqrt{6}\\x=2-\sqrt{6}\Rightarrow y=-3+2\sqrt{6}\end{matrix}\right.\)
Vậy tọa độ giao điểm là: \(\left(2+\sqrt{6};-3-2\sqrt{6}\right)\)
Và \(\left(2-\sqrt{6};-3+2\sqrt{6}\right)\)
\(\left(P\right):y=-x^2+2x+3\\ \left(d\right):y=-2x+1\)
xét phương trình hoành độ giao điểm của (P) và (d)
\(-x^2+2x+3=-2x+1\)
\(< =>-x^2+4x+2=0\)
\(< =>\left[{}\begin{matrix}x=2+\sqrt{6}\\x=2-\sqrt{6}\end{matrix}\right.\)
thay vào (d) => \(\left[{}\begin{matrix}x=2+\sqrt{6}=>y=-3-2\sqrt{6}\\x=2-\sqrt{6}=>y=-3+2\sqrt{6}\end{matrix}\right.\)
vậy ...

a, Bảng biến thiên:
Đồ thị hàm số:
b, Phương trình hoành độ giao điểm
\(-x^2+2x+3=4x-5\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)
Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)

a:
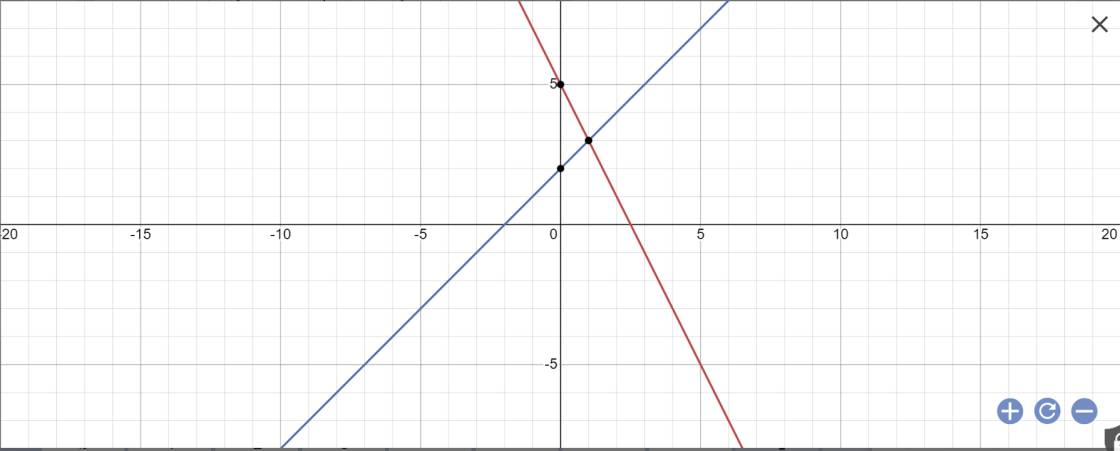
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)

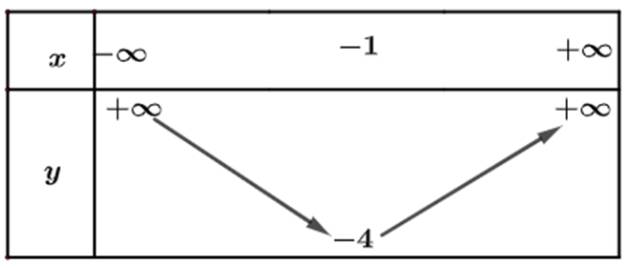
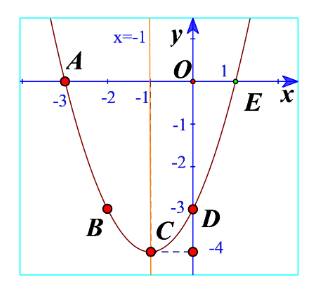
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
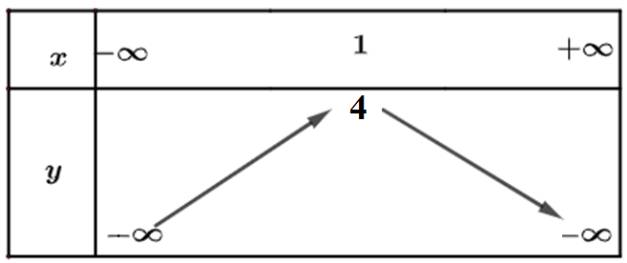
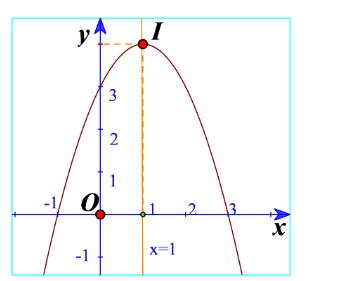
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
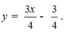
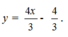
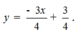
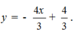

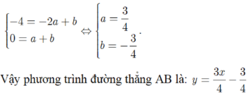
Từ đồ thị hàm số ta có phương trình tổng quát
\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)
Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\)
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\)