Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)
\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)
Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)
Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)
a) \(P=1957\)
b) \(S=19.\)
\(B=\frac{4}{\left|x-5\right|+2012}\) có GTLN
Ta thấy: |x - 5| \(\ge\)0 <=> |x - 5| + 2012 \(\ge\)2012
Nên B = \(\frac{4}{\left|x-5\right|+2012}\le\frac{4}{2012}=\frac{1}{503}\)
Vậy GTLN của B là \(\frac{1}{503}\) khi và chỉ khi |x - 5| = 0 < = > x = 5
Để B đạt GTLN thì \(\frac{4}{\left|x-5\right|+2012}\) phải đạt GTLN
=> \(\frac{4}{\left|x-5\right|+2012}\) phải là số nguyên dương lớn nhất có thể
\(\Rightarrow\left|x-5\right|+2012\) phải đạt GTNN
Ta có:
\(\left|x-5\right|\ge0\Rightarrow\left|x-5\right|+2012\ge2012\)
Dấu "=" xảy ra <=> x - 5 = 0
<=> x = 5
Khi đó, ta đc:
\(B=\frac{4}{2012}=\frac{1}{503}\)
Vậy B đạt GTLN là \(\frac{1}{503}\Leftrightarrow x=5\)
\(P=\sqrt{7-x}+\sqrt{2+x}\ge\sqrt{7-x+2+x}=3\)
\(\Rightarrow P_{min}=3\) khi \(\left[{}\begin{matrix}7-x=0\\2+x=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\)
\(P\le\sqrt{\left(1+1\right)\left(7-x+2+x\right)}=3\sqrt{2}\)
\(\Rightarrow P_{max}=3\sqrt{2}\) khi \(7-x=2+x\Rightarrow x=\frac{5}{2}\)
BĐT \(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\) với các số không âm
Dấu "=" xảy ra khi \(\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\)
Cách chứng minh thì bạn chỉ cần bình phương 2 vế, 1 dòng là xong
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có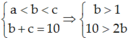 
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
