
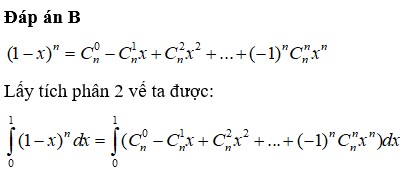
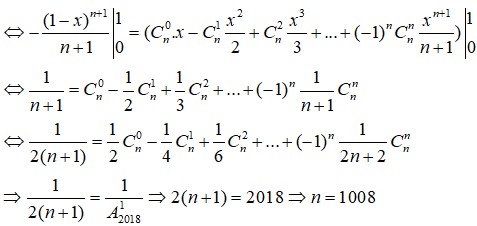
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

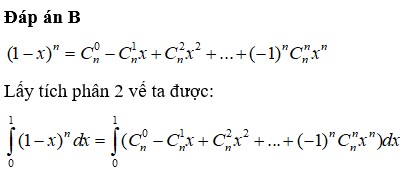
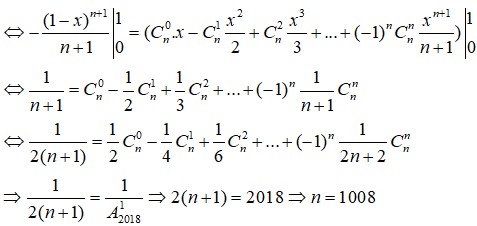

a) 3n + 2 chia hết cho n - 1
\(\Rightarrow\) 3n - 3 + 5 chia hết cho n - 1
\(\Rightarrow\) 3(n - 1) + 5 chia hết cho n - 1
\(\Rightarrow\) 5 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(5) = {-1; 1; -5; 5}
\(\Rightarrow\) n \(\in\) {0; 2; -4; 6}
b) 3n + 24 chia hết cho n - 4
\(\Rightarrow\) 3n - 12 + 36 chia hết cho n - 4
\(\Rightarrow\) 3(n - 4) + 36 chia hết cho n - 4
\(\Rightarrow\) 36 chia hết cho n - 4
\(\Rightarrow\) n - 4 \(\in\) Ư(36) = {-1; 1; -2; 2; -3; 3; -4; 4; -6; 6; -9; 9; -12; 12; -18; 18; -36; 36}
\(\Rightarrow\) n \(\in\) {-3; 5; 4; 6; -1; 7; 0; 8; -2; 10; -5; 13; -8; 16; -14; 22; -32; 40}
c) 3n + 5 chia hết cho n + 1
\(\Rightarrow\) 3n + 3 + 2 chia hết cho n + 1
\(\Rightarrow\) 3(n + 1) + 2 chia hết cho n + 1
\(\Rightarrow\) 2 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(2) = {-1; 1; -2; 2}
\(\Rightarrow\) n \(\in\) {0; 2; -1; 3}

11,
a, 4x-3\(\vdots\) x-2 1
x-2\(\vdots\) x-2\(\Rightarrow\) 4(x-2)\(\vdots\) x-2\(\Rightarrow\) 4x-8\(\vdots\) x-2 2
Từ 1 và 2 ta có:
(4x-3)-(4x-8)\(\vdots\) x-2
\(\Rightarrow\) 4x-3-4x+8\(\vdots\) x-2
\(\Rightarrow\) 5 \(\vdots\) x-2
\(\Rightarrow\) x-2\(\in\) Ư(5)
\(\Rightarrow\) x-2\(\in\){-5;-1;1;5}
\(\Rightarrow\) x\(\in\) {-3;1;3;7}
Vậy......
Phần b và c làm tương tự như phần a pn nhé! ![]()

ĐK: \(n-1\ge4\)
áp dụng công thức tổ hợp và chỉnh hợp ta có
\(\frac{\left(n-1\right)!}{4!\left(n-5\right)!}-\frac{\left(n-1\right)!}{3!\left(n-4\right)!}-\frac{5}{4}\frac{\left(n-2\right)!}{\left(n-4\right)!}=0 \Rightarrow\frac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)}{4!}-\frac{\left(n-1\right)\left(n-2\right)\left(n-3\right)}{3!}-\frac{5}{4}\left(n-2\right)\left(n-3\right)=0\Rightarrow\left(n-2\right)\left(n-3\right)\left(\frac{\left(n-3\right)\left(n-4\right)}{4!}-\frac{n-1}{3!}-\frac{5}{4}\right)=0\)
giải pt đối chiếu với đk của n ta suy ra đc giá trị n cần tìm

a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)