K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MV
19 tháng 2 2016
11,
a, 4x-3\(\vdots\) x-2 1
x-2\(\vdots\) x-2\(\Rightarrow\) 4(x-2)\(\vdots\) x-2\(\Rightarrow\) 4x-8\(\vdots\) x-2 2
Từ 1 và 2 ta có:
(4x-3)-(4x-8)\(\vdots\) x-2
\(\Rightarrow\) 4x-3-4x+8\(\vdots\) x-2
\(\Rightarrow\) 5 \(\vdots\) x-2
\(\Rightarrow\) x-2\(\in\) Ư(5)
\(\Rightarrow\) x-2\(\in\){-5;-1;1;5}
\(\Rightarrow\) x\(\in\) {-3;1;3;7}
Vậy......
Phần b và c làm tương tự như phần a pn nhé! 
CM
11 tháng 12 2019
Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi m , n ∈ ℝ .
Với m = 1 ⇒ d I , P = 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
Với m = - 1 ⇒ d I , P = - 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
⇒ 2 n b + 1 - n 2 c + 4 n 2 + 1 = - 2 n b + 1 - n 2 c + 4 n 2 + 1 ⇔ [ b = 0 1 - n 2 c + 4 n 2 + 1 = 0
Rõ ràng 1 - n 2 c + 4 n 2 + 1 = 0 không thể xảy ra với mọi n ∈ ℝ suy ra b = 0
Với m = n = 1 ⇒ d I , P = b + 4 = R = 4 .
30 tháng 3 2016
Vì n2+5n+9 là bội của n+3
\(\Rightarrow\)n2+5n+9 chia hết cho n+3
\(\Rightarrow n\left(n+3\right)-3n+5n+9\) chia hết cho n+3
\(\Rightarrow n\left(n+3\right)+2n+9\) chia hết cho n+3
\(\Rightarrow n\left(n+3\right)+2\left(n+3\right)-6+9\) chia hết cho n+3
\(\Rightarrow n\left(n+3\right)+2\left(n+3\right)+3\) chia hết cho n+3
Mà \(n\left(n+3\right)+2\left(n+3\right)\) chia hết cho n+3
\(\Rightarrow\)3 chia hết cho n+3
\(\Rightarrow\)n+3 \(\in\) {-3;-1;1;3}
Vì n\(\in\)Z ta có bảng sau:
| n+3 | -3 | -1 | 1 | 3 |
n | 0 | 2 | 4 | 6 |
| Nhận xét | Chọn | Chọn | Chọn | Chọn |
Vậy với n\(\in\){0;2;4;6} thì n2+5n+9 là bội của n+3.
L
17 tháng 2 2016
Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
L
17 tháng 2 2016
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)
27 tháng 1 2016
4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
27 tháng 1 2016
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.
1 tháng 2 2016
x-1 là ước của 2^2-2x+3
=>7-2x chia hết cho x-1
=>2-2x+5 chia hết cho x-1
=>-2.(x-1)+5 chia hết cho x-1
=>5 chia hết cho x-1
=>x-1 thuộc U(5)={1;-1;5;-5}
=>x={2;0;6;-4}
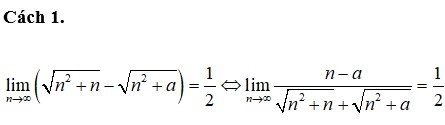
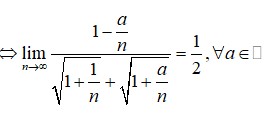
a)n^2-7 \vdots n+3 hay \frac{n^2-7}{n+3}= \frac{(n-3)(n+3)+2}{n+3}= (n-3)+ \frac{2}{n+3} là số nguyên.
Như vậy \frac{2}{n+3} là số nguyên 2 chia hết cho n+3.
a)
hay (n+3)+2}{n+3}=%20(n-3)+%20\frac{2}{n+3} "\frac{n^2-7}{n+3}= \frac{(n-3)(n+3)+2}{n+3}= (n-3)+ \frac{2}{n+3}")
là số nguyên.
là số nguyên 
2 chia hết cho n+3.
Như vậy