Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n 2 - 3 n - 2 n = 0
⇔
n
2
-
5
n
=
0
⇔
n
(
n
-
5
)
=
0
⇔ 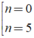
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A

a) Ta có đường chéo là \(\frac{n\left(n-3\right)}{2}\)
Theo đề bài ta có: \(\frac{n\left(n-3\right)}{2}=n\) \(\Leftrightarrow n^2-5n=0\)
\(\Leftrightarrow n\left(n-5\right)=0\)
Vì n \(\ne\) 0, do đó n = 5
Vậy hình ngũ giác lồi có số đường chéo bằng số cạnh
b) Tương tự ta có: \(\frac{n\left(n-3\right)}{2}=\frac{n}{2}\) \(\Leftrightarrow n^2-4n=0\)
\(\Leftrightarrow n\left(n-4\right)=0\)
Vì n \(\ne\) 0, do đó n = 4
Vậy tứ giác lồi có số đường chéo bằng nửa số cạnh
c) Tương tự, ta có: \(\frac{n\left(n-3\right)}{2}=\frac{n}{3}\) \(\Leftrightarrow n\left(3n-11\right)=0\)
Vì n \(\ne\) 0 nên n \(\in\) N bài toán không có lời giải
Vậy không tồn tại đa giác mà số đường chéo bằng một phần ba số cạnh
d) Ta có: \(\frac{n\left(n-3\right)}{2}=2n\) \(\Leftrightarrow n\left(n-7\right)=0\)
Vì n \(\ne\) 0 do đó n = 7
Vậy hình đa giác có 7 cạnh sẽ có số đường chéo bằng hai lần số cạnh
Tồn tại:
a)-ngũ giác có 5 đường chéo
b)-Tứ giác có 2 đường chéo
d)-Thất giác có 14 đường chéo
Không tồn tại:c)

Số đường chéo của đa giác đều n cạnh là \(\dfrac{n\left(n-3\right)}{2}\)
Số đường chéo bằng 33 số cạnh
\(\Rightarrow\dfrac{n\left(n-3\right)}{2}=33n\Rightarrow n\left(n-3\right)=66n\\
\Rightarrow n-3=66\\
\Rightarrow n=69\)
Suy ra đa giác đều đó có 69 cạnh
Số đo mỗi góc là \(\dfrac{180\cdot33+360}{69}\approx91,3\)

Ta có: ( n − 2 ) .180 0 n = 120 0 . Tìm được n = 6 Þ số đường chéo là 9 đường chéo


Gọi số cạnh là n (n ÎN, n ≥3).
a) Ta có: n ( n − 3 ) 2 = n . Tìm được n = 5 (TMĐK)
b) Tìm được n = 4
c) Tìm được n = 7
d) Tìm được n Î Æ