Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11
e: Ta có: \(x^2-6x+y^2+4y+2=0\)
\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Dấu '=' xảy ra khi x=3 và y=-2

\(a,=\left(x+1\right)^2\\ b,=\left(y-2\right)^2\\ c,=\left(x-3\right)^2\\ d,=\left(a-7\right)^2\\ e,=\left(m-2\right)^2\\ f,=\left(2x-1\right)^2\\ g,=\left(a+5\right)^2\\ h,=\left(z-10^2\right)\\ i,=\left(x+3y\right)^2\\ j,=\left(2x-5b\right)^2\\ k,=\left(a+5\right)^2\\ l,=\left(x^2+1\right)^2\\ m,=\left(y^3-1\right)^2=\left(y-1\right)^2\left(y^2+y+1\right)^2\\ n,=\left(c^5-5\right)^2\\ o,=\left(3x^2+2y\right)^2\\ p,=5m^2n^3\left(5m^2n^3-2\right)\)

Bài làm
a) xy + y2 - x - y
= ( xy + y2 ) - ( x + y )
= y( x + y ) - ( x + y )
= ( x + y )( y - 1 )
b) 25 - x2 + 4xy - 4y2
= 25 - ( x2 - 4xy + 4y2 )
= 25 - ( x - 2y )2
= ( 5 - x + 2y )( 5 + x - 2y )
c) xy + xz - 2y - 2z
= ( xy + xz ) - ( 2y + 2z )
= x( y + z ) - 2( y + z )
= ( y + z )( x - 2 )
d) x2 - 6xy + 9y2 - 25z2
= ( x2 - 6xy + 9y2 ) - 25z2
= ( x - 3y )2 - 25z2
= ( x - 3y - 5z )( z - 3y + 5z )
e) 3x2 - 3y2 - 12x + 12y
= 3( x - y )( x + y ) - 12( x - y )
= ( x - y )[ 3( x + y ) - 12 ]
f) 4x3 + 4xy2 + 8x2y - 16x
= 4x( x2 + y2 + 2xy - 4 )
= 4x[ ( x + y)2 - 4 ]
= 4x( x + y - 2 )( x + y + 2 )
g) x2 - 5x + 4
= x2 - x - 4x + 4
= x( x - 1 ) - 4( x - 1 )
= ( x - 1 )( x - 4 )
h) x4 + 5x2 + 4
= x4 + x2 + 4x2 + 4
= x2( x2 + 1 ) + 4( x2 + 1 )
= ( x2 + 1 )( x2 + 4 )
i) 2x2 + 3x - 5
= 2x2 - 5x + 2x - 5
= 2x( x + 1 ) - 5( x + 1 )
= ( x + 1 )( 2x - 5 )
k) x3 - 2x2 + 6x - 5 ( không biết làm )
l) x2 - 4x + 3
= ( x2 - 4x + 4 ) - 1
= ( x - 2 )2 - 1
= ( x - 3 )( x - 1 )
# Học tốt #

\(A=x^3-8-128-x^3=-136\\ B=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)
\(A=\left(x-2\right)\left(x^2+2x+4\right)-\left(128+x^3\right)=x^3-8-128-x^3=-136\)
\(B=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)-\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)

A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
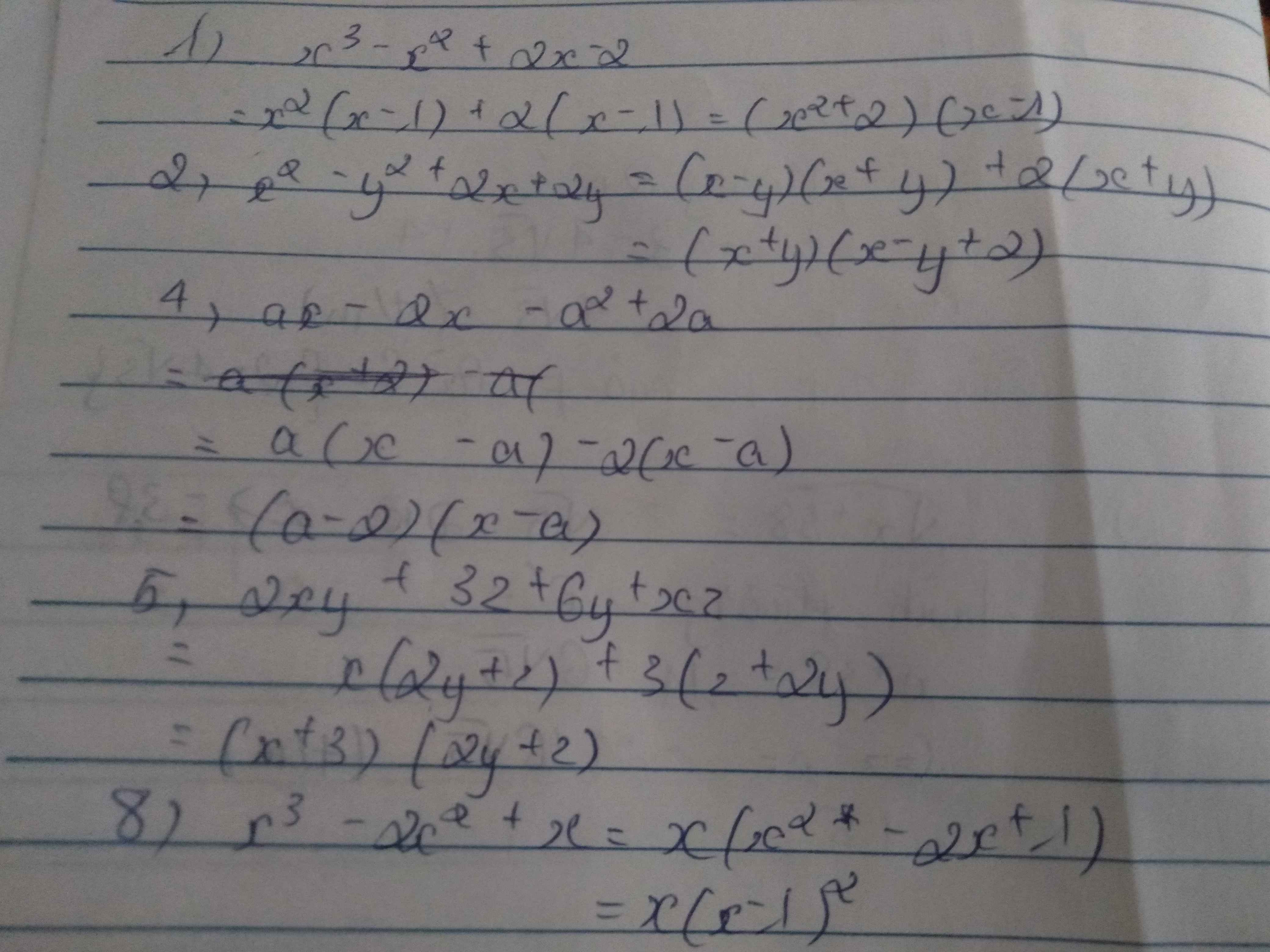
D = 2x2 + 9y2 - 6xy - 6x + 12y + 2012
= [ ( x2 - 6xy + 9y2 ) - 4x + 12y + 4 ] + ( x2 - 2x + 1 ) + 2007
= [ ( x - 3y )2 - 2( x - 3y ).2 + 22 ] + ( x - 1 )2 + 2007
= ( x - 3y + 2 )2 + ( x - 1 )2 + 2007
\(\hept{\begin{cases}\left(x-3y+2\right)^2\\\left(x-1\right)^2\end{cases}}\ge0\forall x\Rightarrow\left(x-3y+2\right)^2+\left(x-1\right)^2+2007\ge2007\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-3y+2=0\\x-1=0\end{cases}}\Rightarrow x=y=1\)
=> MinD = 2007 <=> x = y = 1
E = x2 - 2xy + 4y2 - 2x - 10y + 29 ( -10y mới ra đc nhé, mò mãi :v )
= [ ( x2 - 2xy + y2 ) - 2x + 2y + 1 ] + ( 3y2 - 12y + 12 ) + 16
= [ ( x - y )2 - 2( x - y ) + 12 ] + 3( y2 - 4y + 4 ) + 16
= ( x - y - 1 )2 + 3( y - 2 )2 + 16
\(\hept{\begin{cases}\left(x-y-1\right)^2\\3\left(y-2\right)^2\end{cases}}\ge0\forall x,y\Rightarrow\left(x-y-1\right)^2+3\left(y-2\right)^2+16\ge16\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\Rightarrow\hept{\begin{cases}x=3\\y=2\end{cases}}\)
=> MinE = 16 <=> x = 1 ; y = 2
F = \(\frac{3}{2x-x^2-4}\)
Để F đạt GTNN => 2x - x2 - 4 đạt GTLN
Ta có : 2x - x2 - 4 = -( x2 - 2x + 1 ) - 3 = -( x - 1 )2 - 3 ≤ -3 < 0 ∀ x
Đẳng thức xảy ra <=> x - 1 = 0 => x = 1
=> MinF = \(\frac{3}{-3}=-1\)<=> x = 1
G = \(\frac{2}{6x-5-9x^2}\)
Để G đạt GTNN => 6x - 5 - 9x2 đạt GTLN
Ta có 6x - 5 - 9x2 = -9( x2 - 2/3x + 1/9 ) - 4 = -9( x - 1/3 )2 - 4 ≤ -4 < 0 ∀ x
Đẳng thức xảy ra <=> x - 1/3 = 0 => x = 1/3
=> MinG = \(\frac{2}{-4}=-\frac{1}{2}\)<=> x = 1/3