PV
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
18 tháng 12 2023
Lời giải:
a. $3x^2-9x=3x(x-3)$
b. $4x^2+7y-4xy-7x=(4x^2-4xy)-(7x-7y)=4x(x-y)-7(x-y)=(x-y)(4x-7)$
CM
19 tháng 12 2017
⇒
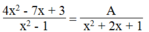4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒ 4 x 2 - 4 x - 3 x + 3 x + 1 2 = A x + 1 x - 1
⇒ 4 x x - 1 - 3 x - 1 . x + 1 2 = A . x + 1 x - 1
⇒ x - 1 4 x - 3 x + 1 2 = A x + 1 x - 1
⇒ A = 4 x - 3 x + 1 = 4 x 2 + 4 x - 3 x - 3 = 4 x 2 + x - 3
Vậy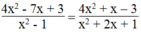 
18 tháng 1 2017
\(A_{min}=8-\frac{25}{4}\) khi x=5/2
Bmin=xem lại đề đúng như đề Bmin=5 khi x=0
C=8+25-(2x+5)^2
Cmax=8+25 khi x=-5/2
Dmax=9 khi x=0
NH
3
ND
Nguyễn Đức Trí
VIP
19 tháng 8 2023
\(E=-4x^2+x+1\)
\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}\right)+1\)
\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}+\dfrac{1}{64}\right)+1+\dfrac{1}{16}\)
\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\)
mà \(-4\left(x-\dfrac{1}{8}\right)^2\le0,\forall x\)
\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\le\dfrac{17}{16}\)
\(\Rightarrow GTLN\left(E\right)=\dfrac{17}{16}\left(tạix=\dfrac{1}{8}\right)\)
ND
Nguyễn Đức Trí
VIP
19 tháng 8 2023
\(F=5x-3x^2+6\)
\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}\right)+6\)
\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}+\dfrac{25}{36}\right)+6+\dfrac{25}{12}\)
\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\)
mà \(-3\left(x-\dfrac{5}{6}\right)^2\le0,\forall x\)
\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\le\dfrac{97}{12}\)
\(\Rightarrow GTLN\left(F\right)=\dfrac{97}{12}\left(tạix=\dfrac{5}{6}\right)\)
18 tháng 1 2017
Cụ thể mức nào nhỉ tất cả dự trên HĐT \(\left(a+-b\right)^2=a^2+-2ab+b^2\)
cụ thể con A
\(A=x^2-2.\frac{5}{2}x+\left(\frac{5^2}{2^2}\right)+8-\frac{25}{4}\) đã thêm 25/4 =b vào phần đầu => trừ đi
\(A=\left(x-\frac{5}{2}\right)^2+8-\frac{25}{4}=\left(x-\frac{5}{2}\right)^2+\frac{7}{4}\)
\(\left(x-\frac{5}{2}\right)^2\ge0\Rightarrow A\ge\frac{7}{4}\)đẳng thức khi x-5/2=0=> x=5/2
18 tháng 1 2017
A=(x-5/2)^2+8-25/4=> Amin=7/4 khi x=5/2
B --> xem lại theo đề Bmin =5 khi x=0
C =8+25-(2x+5)^2=> C max=32 khi x=-5/2
D max=9 khi x=0
20 tháng 1 2017
a, 3x2 - 8x2 - 2x+3=0
2x(3-8) - 2x+3=0
2x5 - 2x+3=0
2x5 - 2x=0-3=
2x5 - 2x=-3
2x(5-x)=-3
5-x=-3/2
5-x=1,5
x=5-1,5
x=3,5
30 tháng 10 2021
a) \(5x+10y=5\left(x+2y\right)\)
b) \(3x^3-12x=3x\left(x^2-4\right)=3x\left(x-2\right)\left(x+2\right)\)
c) \(4x^2+9x-4xy-9y=4x\left(x-y\right)+9\left(x-y\right)=\left(x-y\right)\left(4x+9\right)\)
d) \(3x^2+5y-3xy-5x=3x\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(3x-5\right)\)
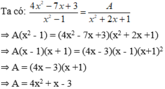
\(C=-4x^2+9x+7=-\left[\left(2x\right)^2-9x-7\right]\)
\(=-\left[\left(2x\right)^2-2.2,25x+5,0625-12,0625\right]\)
\(=-\left[\left(2x-2,25\right)^2-12,065\right]=-\left(2x-2,25\right)^2+12,0625\)
Ta có: \(\left(2x-2,25\right)^2\ge0\)\(\Leftrightarrow-\left(2x-2,25\right)^2\le0\)\(\Leftrightarrow-\left(2x-2,25\right)^2+12,0625\le12,0625\)
Vậy \(C_{max}=12,0625\)(Dấu "="\(\Leftrightarrow x=1,125\))
C= -4x2 +9x+7
Giải phương trình trên máy tính rồi ấn 3 lần dấu ' = ' để tìm GTLN
KQ : Max C = \(\frac{9}{8}\)
D=-3x2-7x+12
Giải phương trình trên máy tính rồi ấn 3 lần dấu ' = ' để tìm GTLN
Max D = \(-\frac{7}{6}\)
Không có Min đâu nhé bạn