Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Bài 2:
a: TH1: m=0
=>-x+1=0
=>x=-1(nhận)
TH2: m<>0
\(\text{Δ}=\left(m-1\right)^2-4m\left(1-m\right)\)
=m^2-2m+1-4m+4m^2
=5m^2-6m+1
=(2m-1)(3m-1)
Để phương trình có nghiệm thì (2m-1)(3m-1)>=0
=>m>=1/2 hoặc m<=1/3
b: Để phương trình có hai nghiệm phân biệt thì (2m-1)(3m-1)>0
=>m>1/2 hoặc m<1/3
c: Để phương trình có hai nghiệmtrái dấu thì (1-m)*m<0
=>m(m-1)>0
=>m>1 hoặc m<0
d: Để phương trình có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\\dfrac{-m+1}{m}>0\\\dfrac{1-m}{m}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\0< m< 1\end{matrix}\right.\)
=>1/2<m<1

\(mx^2+\left(m-1\right)x+3-4m=0\left(1\right)\)
\(m=0\Rightarrow\)\(\left(1\right)\Leftrightarrow-x+3=0\Leftrightarrow x=3\left(ktm\right)\)
\(m\ne0\Rightarrow x1< 2< x2\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-2\right)\left(x2-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2-4m\left(3-4m\right)>0\\x1x2-2\left(x1+x2\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\\dfrac{3-4m}{m}-2.\left(\dfrac{1-m}{m}\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\-\dfrac{1}{2}< m< 0\\\end{matrix}\right.\)\(\Rightarrow m\in\phi\)

1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\\Delta=\left(2m-1\right)^2-4m\left(m-2\right)>0\\x_1+x_2=\dfrac{1-2m}{m}< 0\\x_1x_2=\dfrac{m-2}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\4m+1>0\\\dfrac{1-2m}{m}< 0\\\dfrac{m-2}{m}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{4}\\\left[{}\begin{matrix}m< 0\\m>\dfrac{1}{2}\end{matrix}\right.\\\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{4}< m< 0\\m>2\end{matrix}\right.\)

a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)

a. Với \(m=0\Rightarrow-x-1=0\Rightarrow x=-1\) pt có nghiệm (ktm)
Với \(m\ne0\) pt vô nghiệm khi:
\(\Delta=\left(m-1\right)^2-4m\left(m-1\right)< 0\)
\(\Leftrightarrow\left(m-1\right)\left(-3m-1\right)< 0\)
\(\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)
b. Phương trình có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Leftrightarrow m\left(m-1\right)< 0\Rightarrow0< m< 1\)
c. Từ câu a ta suy ra pt có 2 nghiệm khi \(\left\{{}\begin{matrix}m\ne0\\-\dfrac{1}{3}\le m\le1\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1-m}{m}\\x_1x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
\(x_1^2+x_2^2-3>0\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-3>0\)
\(\Leftrightarrow\left(\dfrac{1-m}{m}\right)^2-2\left(\dfrac{m-1}{m}\right)-3>0\)
Đặt \(\dfrac{m-1}{m}=t\Rightarrow t^2-2t-3>0\Rightarrow\left[{}\begin{matrix}t>3\\t< -1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{m-1}{m}>3\\\dfrac{m-1}{m}< -1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{-2m-1}{m}>0\\\dfrac{2m-1}{m}< 0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{2}< m< 0\\0< m< \dfrac{1}{2}\end{matrix}\right.\)
Kết hợp điều kiện có nghiệm \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}\le m< 0\\0< m< \dfrac{1}{2}\end{matrix}\right.\)

a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)

a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 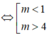
Do x1 < x2 < 1
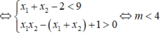
Bài 2:
a: TH1: m=0
Pt sẽ là \(-\left(2\cdot0+1\right)x+0-5=0\)
=>-x-5=0
=>x=-5(loại)
TH2: m<>0
\(\text{Δ}=\left(2m+1\right)^2-4m\left(m-5\right)\)
=4m^2+4m+1-4m^2+20m
=24m+1
Để pt vô nghiệm thì 24m+1<0
=>m<-1/24
b: TH1: m=3
Pt sẽ là (3-3)*x^2+2(3-3)*x+3+1=0
=>4=0(loại)
TH2: m<>3
\(\text{Δ}=\left(6-2m\right)^2-4\left(m-3\right)\left(m+1\right)\)
\(=4m^2-24m+36-4\left(m^2-2m-3\right)\)
\(=4m^2-24m+36-4m^2+8m+12=-16m+48\)
Để phương trình vônghiệm thì -16m+48<0
=>-16m<-48
=>m>3