
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

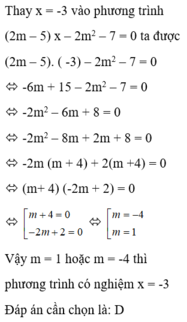

Bài 5 :
Thay \(x=-3\) vào pt : \(3x+m-x-1=0\)
\(\Leftrightarrow3\left(-3\right)+m-\left(-3\right)-1=0\)
\(\Leftrightarrow-9+m+3-1=0\)
\(\Leftrightarrow m-7=0\)
\(\Leftrightarrow m=7\)
Vậy \(m=7\) để pt nhận \(x=-3\) là nghiệm
Bài 6 :
Thay \(x=1\) vào pt : \(\left(2m-4\right)x+6=0\)
\(\Leftrightarrow2mx-4x+6=0\)
\(\Leftrightarrow2m-4+6=0\)
\(\Leftrightarrow2m+2=0\)
\(\Leftrightarrow m=-1\)
Vậy \(m=-1\) để pt nhận \(x=1\) là nghiệm

\(a,PT\Leftrightarrow\left(1-2m\right)x=m+4\)
Bậc nhất \(\Leftrightarrow1-2m\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
\(b,x=2\Leftrightarrow2-4m-m-4=0\Leftrightarrow m=-\dfrac{2}{5}\\ c,m=5\Leftrightarrow-9x-9=0\Leftrightarrow x=-1\)

Bài 1:
c) ĐKXĐ: \(x\notin\left\{\dfrac{1}{4};-\dfrac{1}{4}\right\}\)
Ta có: \(\dfrac{3}{1-4x}=\dfrac{2}{4x+1}-\dfrac{8+6x}{16x^2-1}\)
\(\Leftrightarrow\dfrac{-3\left(4x+1\right)}{\left(4x-1\right)\left(4x+1\right)}=\dfrac{2\left(4x-1\right)}{\left(4x+1\right)\left(4x-1\right)}-\dfrac{6x+8}{\left(4x-1\right)\left(4x+1\right)}\)
Suy ra: \(-12x-3=8x-2-6x-8\)
\(\Leftrightarrow-12x-3-2x+10=0\)
\(\Leftrightarrow-14x+7=0\)
\(\Leftrightarrow-14x=-7\)
\(\Leftrightarrow x=\dfrac{1}{2}\)(nhận)
Vậy: \(S=\left\{\dfrac{1}{2}\right\}\)

a) Khi \(m=-4\) phương trình trở thành:
\(\left[\left(-4\right)^2+5.\left(-4\right)+4\right]x^2=-4+4\)
\(\Leftrightarrow0.x^2=0\)
Đúng với mọi x.
b) Khi \(m=-1\) phương trình trở thành:
\(\left[\left(-1\right)^2+5.\left(-1\right)+4\right]x^2=-1+4\)
\(\Leftrightarrow0.x^2=3\)
Phương trình vô nghiệm.
c) Khi \(m=-2\) phương trình trở thành:
\(\left[\left(-2\right)^2+5.\left(-2\right)+4\right]x^2=-2+4\)
\(\Leftrightarrow-2.x^2=2\)
\(\Leftrightarrow x^2=-1\)
Phương trình này cũng vô nghiệm.
Khi \(m=-3\) phương trình trở thành:
\(\left[\left(-3\right)^2+5.\left(-3\right)+4\right]x^2=-3+4\)
\(\Leftrightarrow-2x^2=1\)
\(\Leftrightarrow x^2=-\dfrac{1}{2}\)
Phương trình cũng vô nghiệm.
d) Khi \(m=0\) phương trình trở thành:
\(\left[0^2+5.0+4\right]x^2=0+4\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
Phương trình có hai nghiệm là \(x=1,x=-1\).

\(1.A=x^2+3x-1=-\left(x^2-2.x.\frac{3}{2}+\frac{3}{2}^2-\frac{5}{4}\right)\)
\(A=-\left(x-\frac{3}{2}\right)^2+\frac{5}{4}\)
Vì \(\left(x-\frac{3}{2}\right)^2\ge0,x\in R\)
do đó \(-\left(x-\frac{3}{2}\right)^2\le0,x\in R\)
nên \(-\left(x-\frac{3}{2}\right)^2+\frac{5}{4}\le\frac{5}{4},x\in R\)
Vậy \(Max_A=\frac{5}{4},x=\frac{3}{2}\)

a) Ta có: \(x^2+\dfrac{9x^2}{\left(x+3\right)^2}=40\)
\(\Leftrightarrow\dfrac{\left(x^2+3x\right)^2+9x^2}{\left(x+3\right)^2}=40\)
\(\Leftrightarrow x^4+6x^3+9x^2+9x^2=40\left(x+3\right)^2\)
\(\Leftrightarrow x^4+6x^3+18x^2=40\left(x^2+6x+9\right)\)
\(\Leftrightarrow x^4+6x^3+18x^2-40x^2-240x-360=0\)
\(\Leftrightarrow x^4+6x^3-22x^2-240x-360=0\)
\(\Leftrightarrow x^4+2x^3+4x^3+8x^2-30x^2-60x-180x-360=0\)
\(\Leftrightarrow x^3\left(x+2\right)+4x^2\left(x+2\right)-30x\left(x+2\right)-180\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3+4x^2-30x-180\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3-6x^2+10x^2-60x+30x-180\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x^2\left(x-6\right)+10x\left(x-6\right)+30\left(x-6\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\cdot\left(x-6\right)\left(x^2+10x+30\right)=0\)
mà \(x^2+10x+30>0\forall x\)
nên \(\left(x+2\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=6\end{matrix}\right.\)
Vậy: S={-2;6}
b) Ta có: (m-1)x+3m-2=0
\(\Leftrightarrow\left(m-1\right)x=2-3m\)
\(\Leftrightarrow x=\dfrac{2-3m}{m-1}\)
Để phương trình có nghiệm duy nhất thỏa mãn \(x\ge1\) thì \(\dfrac{2-3m}{m-1}\ge1\)
\(\Leftrightarrow\dfrac{2-3m}{m-1}-1\ge0\)
\(\Leftrightarrow\dfrac{2-3m-\left(m-1\right)}{m-1}\ge0\)
\(\Leftrightarrow\dfrac{2-3m-m+1}{m-1}\ge0\)
\(\Leftrightarrow\dfrac{-4m+3}{m-1}\ge0\)
hay \(\dfrac{3}{4}\le m< 1\)
Vậy: Để phương trình (m-1)x+3m-2=0 có nghiệm duy nhất thỏa mãn \(x\ge1\) thì \(\dfrac{3}{4}\le m< 1\)