Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả thiết tương đương:
\(C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{100}\) (thay \(1=C_{2n+1}^{2n+1}\))
Mặt khác:
\(C_{2n+1}^{2n+1}=C_{2n+1}^0\)
\(C_{2n+1}^{2n}=C_{2n+1}^1\)
....
\(C_{2n+1}^{n+1}=C_{2n+1}^n\)
Cộng vế:
\(\Rightarrow C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n\)
\(\Rightarrow2\left(C_{2n+1}^{n+1}+...+C_{2n+1}^{2n+1}\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n+1}\)
\(\Rightarrow2.2^{100}=2^{2n+1}\) (đẳng thức cơ bản: \(\sum\limits^n_{k=0}C_n^k=2^n\))
\(\Leftrightarrow2^{101}=2^{2n+1}\)
\(\Rightarrow2n+1=101\)
\(\Rightarrow n=50\)
SHTQ trong khai triển: \(C_{50}^k.\left(x^{-3}\right)^k.\left(x^2\right)^{50-k}=C_{50}^kx^{100-5k}\)
\(100-5k=20\Rightarrow k=16\)
Hệ số: \(C_{50}^{16}\)

Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)

Câu 2:
\(\Leftrightarrow\dfrac{\left(n+2\right)!}{2!\cdot n!}-4\cdot\dfrac{\left(n+1\right)!}{n!\cdot1!}=2\left(n+1\right)\)
\(\Leftrightarrow\dfrac{\left(n+1\right)\left(n+2\right)}{2}-4\cdot\dfrac{n+1}{1}=2\left(n+1\right)\)
\(\Leftrightarrow\left(n+1\right)\left(n+2\right)-8\left(n+1\right)=4\left(n+1\right)\)
=>(n+1)(n+2-8-4)=0
=>n=-1(loại) hoặc n=10
=>\(A=\left(\dfrac{1}{x^4}+x^7\right)^{10}\)
SHTQ là: \(C^k_{10}\cdot\left(\dfrac{1}{x^4}\right)^{10-k}\cdot x^{7k}=C^k_{10}\cdot1\cdot x^{11k-40}\)
Số hạng chứa x^26 tương ứng với 11k-40=26
=>k=6
=>Số hạng cần tìm là: \(210x^{26}\)

\(C^n_n+C^{n-1}_n+C^{n-2}_n=37\)
\(\Leftrightarrow1+\dfrac{n!}{\left(n-1\right)!}+\dfrac{n!}{\left(n-2\right)!2!}=37\)
\(\Leftrightarrow1+n+\dfrac{n\left(n-1\right)}{2}=37\)
\(\Rightarrow n=8\)
\(P=\left(2+5x\right)\left(1-\dfrac{x}{2}\right)^8=\left(2+5x\right).\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{x}{2}\right)^k\right)\)
\(=\left(2+5x\right).\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\)
\(=2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)+5x\)\(\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\)
\(=2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)+5\)\(\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^{k+1}\right)\)
Số hạng chứa \(x^3\) trong \(2.\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^k\right)\) là \(2C^3_8.\left(-\dfrac{1}{2}\right)^3x^3\)
Số hạng chứa \(x^3\) trong \(5\left(\sum\limits^8_{k=0}.C_8^k.\left(-\dfrac{1}{2}\right)^k.x^{k+1}\right)\) là \(5C^2_8.\left(-\dfrac{1}{2}\right)^2x^3\)
Vậy số hạng chứa x3 trong P là:\(\left[2.C^3_8\left(-\dfrac{1}{2}\right)^3+5C^2_8\left(-\dfrac{1}{2}\right)^2\right]x^3\)

\(\left(C_n^6+C_n^7\right)+2\left(C_n^7+C_n^8\right)+\left(C_n^8+C_n^9\right)=2C_{n+2}^8\)
\(\Leftrightarrow C_{n+1}^7+2C_{n+1}^8+C_{n+1}^9=2C_{n+2}^8\)
\(\Leftrightarrow\left(C_{n+1}^7+C_{n+1}^8\right)+\left(C_{n+1}^8+C_{n+1}^9\right)=2C_{n+2}^8\)
\(\Leftrightarrow C_{n+2}^8+C_{n+2}^9=2C_{n+2}^8\)
\(\Leftrightarrow C_{n+2}^9=C_{n+2}^8\)
\(\Leftrightarrow n+2=9+8\)
\(\Rightarrow n=15\)
\(\left(x^2-\dfrac{1}{x^2}\right)^{15}\) có SHTQ: \(C_{15}^kx^{2k}.\left(-1\right)^{15-k}.x^{2k-30}=C_{15}^k.\left(-1\right)^{15-k}.x^{4k-30}\)
Số hạng ko chứa x \(\Rightarrow4k-30=0\) ko có k nguyên thỏa mãn
\(\Rightarrow\) Ko tồn tại số hạng ko chứa x
Đề bài sai

Ta có:
\(2A_n^2=C_{n-1}^2+C_{n-1}^3\) \(\left(n\ge4\right)\)
\(\Rightarrow2\cdot\dfrac{n!}{\left(n-2\right)!}=\dfrac{\left(n-1\right)!}{2!\left(n-1-2\right)!}+\dfrac{\left(n-1\right)!}{3!\left(n-1-3\right)!}\)
\(\Rightarrow2\cdot n\left(n-1\right)=\dfrac{\left(n-1\right)\left(n-2\right)}{4}+\dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow2n=\dfrac{n-2}{4}+\dfrac{\left(n-2\right)\left(n-3\right)}{6}\)
\(\Rightarrow n=14\) hoặc \(n=0\left(loại\right)\)
Với n=14 ta có khai triển:
\(\left(x^2-\dfrac{1}{x^2}\right)^{14}=\sum\limits^{14}_{k=0}\cdot C_{14}^k\cdot\left(x^2\right)^{14-k}\cdot\left(\dfrac{1}{x^2}\right)^k\)
\(=C_{14}^k\cdot x^{28-4k}\)
Số hạng không chứa x: \(\Rightarrow28-4k=0\Rightarrow k=7\)
Vậy số hạng không chứa x trong khai triển là:
\(C_{14}^7\cdot x^{28-4\cdot7}=C_{14}^7=3432\)

\(\left(x^{-\frac{2}{3}}+x^{\frac{3}{4}}\right)^{17}=\sum\limits^{17}_{k=0}C_{17}^k\left(x^{-\frac{2}{3}}\right)^k\left(x^{\frac{3}{4}}\right)^{17-k}=\sum\limits^{17}_{k=0}C_{17}^kx^{\frac{51}{4}-\frac{17}{12}k}\)
Số hạng thứ 13 \(\Rightarrow k=12\) là: \(C_{17}^{12}x^{-\frac{17}{4}}\)
b/ Xét khai triển:
\(\left(3-x\right)^n=C_n^03^n+C_n^13^{n-1}\left(-x\right)^1+C_n^23^{n-2}\left(-x\right)^2+...+C_n^n\left(-x\right)^n\)
Cho \(x=1\) ta được:
\(2^n=3^nC_n^0-3^{n-1}C_n^1+3^{n-2}C_n^2+...+\left(-1\right)^nC_n^n\)
À, đến đây mới thấy đề thiếu, biết rằng cái kia làm sao hả bạn?
 câu 1
câu 1
Chọn C
Ta có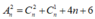
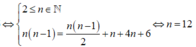 .
.
Xét khai triển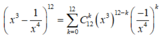
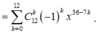 .
.
Số hạng chứa x 8 tương ứng với 36 - 7k = 8 => k = 4.
Vậy hệ số của số hạng chứa x 8 trong khai triển x 3 - 1 x 4 n bằng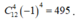 .
.