Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}\)
\(\dfrac{y}{4}=\dfrac{z}{5}\Rightarrow\dfrac{y}{12}=\dfrac{z}{15}\)
\(\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.8=16\\y=2.12=24\\z=2.15=30\end{matrix}\right.\)
a) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/3 = y/4 = x/3 + y/4 = 28/7 = 4
=> x = 4 × 3 = 12
=> y = 4 × 4 = 16
Vậy x = 12, y = 16
B) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/2 = y/(-5) = x/2 - y/(-5) = (-7)/7 = -1
=> x = -1 × 2 = -2
=> y = -1 × -5 = 5
Vậy x = -2, y = 5
C) làm tương tự như bài a, b
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
x8=y12=z15=x+y−z8+12−15=105=2x8=y12=z15=x+y−z8+12−15=105=2
Do đó: x=16; y=24; z=30
Đặt k = 
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10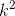 
= 10 => 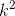= 1 => k = ± 1
Với k = 1 ta được = 1 suy ra x = 2, y = 5
Với k = -1 ta được = -1 suy ra x = -2, y = -5
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{28}{7}=4\)
Do đó: x=12; y=16
\(a,Sửa:\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{28}{7}=4\\ \Rightarrow\left\{{}\begin{matrix}x=12\\y=16\end{matrix}\right.\\ b,\Rightarrow\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2+5}=\dfrac{-7}{7}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{15}=\dfrac{x+3y-5z}{4+3\cdot6-5\cdot15}=\dfrac{-106}{-53}=2\)
Do đó: x=8; y=12; z=30
a) \(x + y = 30;\dfrac{x}{2} = \dfrac{y}{3}\) áp dụng tính chất của tỉ lệ thức ra có :
\( \Rightarrow \dfrac{{x + y}}{{2 + 3}} = \dfrac{x}{2}\)
\( \Rightarrow \dfrac{{30}}{5} = \dfrac{x}{2}\)
\( \Rightarrow 30.2 = x.5\)
\(\begin{array}{l} \Rightarrow 60:5 = x\\ \Rightarrow x = 12\\ \Rightarrow 14 + y = 30\\ \Rightarrow y = 18\end{array}\) ( thay x vừa tìm được = 12 vào x + y = 30 để tìm ra y )
Vậy x = 12 y = 18
b) Ta có : \(\dfrac{x}{5} = \dfrac{y}{{ - 2}}\)= \(\dfrac{{x - y}}{{5 + 2}}\)( áp dụng tính chất tỉ lệ thức ) (1)
Mà theo đề bài x – y = -21
Thay -21 vào (1) ta có : \(\dfrac{{ - 21}}{7} = - 3\) \( = \dfrac{x}{5}\)
\( \Rightarrow \)x = (-3).5
\( \Rightarrow \)x = -15
Thay x bằng -15 ta có -15 – y = -21
\( \Rightarrow \)y = -15 + 21
\( \Rightarrow \)y = 6
Vậy x = -15 và y = 6
\(\dfrac{x}{5}=\dfrac{y}{2}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=5k\\y=2k\end{matrix}\right.\)
\(\Rightarrow xy=10k^2=1000\Rightarrow k=\pm10\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=50\\y=20\end{matrix}\right.\\\left\{{}\begin{matrix}x=-50\\y=-20\end{matrix}\right.\end{matrix}\right.\)
a. Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3$
$\Rightarrow x=2(-3)=-6; y=5(-3)=-15$
b. Áp dụng tính chất dãy tỉ số bằng nhau:
$7x=3y=\frac{x}{\frac{1}{7}}=\frac{y}{\frac{1}{3}}=\frac{x-y}{\frac{1}{7}-\frac{1}{3}}=\frac{16}{\frac{-4}{21}}=-84$
$\Rightarrow x=(-84):7=-12; y=-84:3=-28$
c. $\frac{x}{y}=\frac{5}{9}\Rightarrow \frac{x}{5}=\frac{y}{9}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{5}=\frac{y}{9}=\frac{3x}{15}=\frac{2y}{18}=\frac{3x+2y}{15+18}=\frac{66}{33}=2$
$\Rightarrow x=2.5=10; y=9.2=18$
d. Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{15}=\frac{y}{7}=\frac{2y}{14}=\frac{x-2y}{15-14}=\frac{16}{1}=16$
$\Rightarrow x=16.15=240; y=7.16=112$
e.
Đặt $\frac{x}{5}=\frac{y}{2}=k\Rightarrow x=5k ; y=2k$
Khi đó: $xy=5k.2k=10k^2=1000\Rightarrow k^2=100\Rightarrow k=\pm 10$
Với $k=10$ thì $x=5k=50; y=2k=20$
Với $k=-10$ thì $x=5k=-50; y=2k=-20$
Lời giải:
Đặt $\frac{x}{2}=\frac{y}{5}=k$
$\Rightarrow x=2k; y=5k$. Khi đó:
$xy=2k.5k=10$
$10k^2=10$
$k^2=1$
$\Rightarrow k=\pm 1$
Nếu $k=1$ thì $x=2k=2; y=5k=5$
Nếu $k=-1$ thì $x=2k=-2; y=5k=-5$
Em cảm ơn thầy (cô) ạ